A-Level Maths Edexcel 9MA0
Paper 1 - Jun 2018 9MA0/01
Time allowed: 2 h 0 min.
The total mark for this paper is 100.
The marks for each question are shown in brackets [ ].
1.
Given that θ is small and is measured in radians, use the small angle approximations to find an approximate value of
\[\dfrac{1 - \cos{4θ}}{2θ\sin{3θ}}\]
\[\dfrac{1 - \cos{4θ}}{2θ\sin{3θ}}\]
[3]

2.
A curve C has equation
\[y=x^2−2x−24\sqrt{x}, \qquad x>0\]
(a) Find
(i) \(\dfrac{dy}{dx}\)
(ii) \(\dfrac{d^2y}{dx^2}\)
(b) Verify that C has a stationary point when \(x=4\)
(c) Determine the nature of this stationary point, giving a reason for your answer.
\[y=x^2−2x−24\sqrt{x}, \qquad x>0\]
(a) Find
(i) \(\dfrac{dy}{dx}\)
(ii) \(\dfrac{d^2y}{dx^2}\)
[3]
(b) Verify that C has a stationary point when \(x=4\)
[2]
(c) Determine the nature of this stationary point, giving a reason for your answer.
[2]
[7]
Differentiation of standard functions Turning points
3.
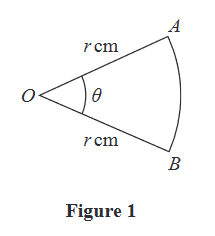
Figure 1 shows a sector AOB of a circle with centre O and radius r cm.
The angle AOB is θ radians.
The area of the sector AOB is 11 cm2
Given that the perimeter of the sector is 4 times the length of the arc AB, find the exact value of r.
[4]

4.
The curve with equation \({y=2\ln{(8−x)}} \) meets the line \({y=x}\) at a single point, \({x=α}\).
(a) Show that \(3 < α < 4 \)
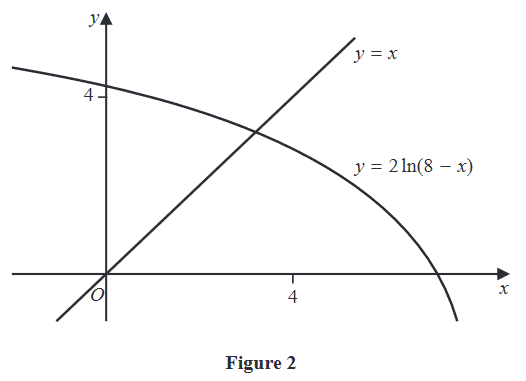
Figure 2 shows the graph of \({y=2\ln{(8−x)}} \) and the graph of \({y=x}\).
A student uses the iteration formula
\[x_{n+1} = 2\ln{(8 - x_n)}, \qquad n∈ℕ \]
in an attempt to find an approximation for \(α\)
Using the graph and starting with \(x_1 = 4\)
(b) determine whether or not this iteration formula can be used to find an approximation for \(α\), justifying your answer.
(a) Show that \(3 < α < 4 \)
[2]

Figure 2 shows the graph of \({y=2\ln{(8−x)}} \) and the graph of \({y=x}\).
A student uses the iteration formula
\[x_{n+1} = 2\ln{(8 - x_n)}, \qquad n∈ℕ \]
in an attempt to find an approximation for \(α\)
Using the graph and starting with \(x_1 = 4\)
(b) determine whether or not this iteration formula can be used to find an approximation for \(α\), justifying your answer.
[2]
[4]
5.
Given that
\[y = \dfrac{3\sin{θ}}{2\sin{θ} + 2\cos{θ}} \qquad -\dfrac{π}{4} < θ < \dfrac{3π}{4} \]
show that
\[\dfrac{dy}{dθ} = \dfrac{A}{1 + \sin{2θ}} \qquad -\dfrac{π}{4} < θ < \dfrac{3π}{4} \]
where A is a rational constant to be found.
\[y = \dfrac{3\sin{θ}}{2\sin{θ} + 2\cos{θ}} \qquad -\dfrac{π}{4} < θ < \dfrac{3π}{4} \]
show that
\[\dfrac{dy}{dθ} = \dfrac{A}{1 + \sin{2θ}} \qquad -\dfrac{π}{4} < θ < \dfrac{3π}{4} \]
where A is a rational constant to be found.
[5]

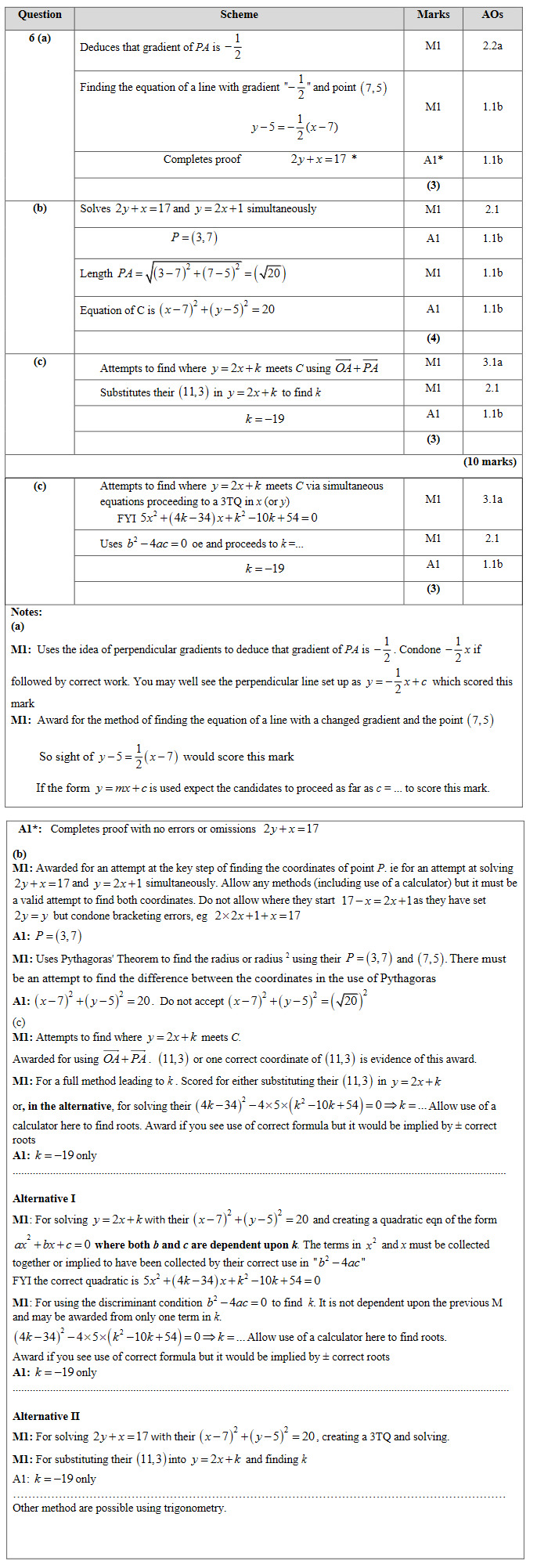
6.

The circle C has centre A with coordinates (7, 5).
The line l, with equation \(y=2x+1\), is the tangent to C at the point P, as shown in Figure3.
(a) Show that an equation of the line PA is \(2y + x = 17\)
[3]
(b) Find an equation for C.
[4]
The line with equation \(y=2x+k, \quad k≠1\) is also a tangent to C.
(c) Find the value of the constant k.
[3]
[10]
7.
Given that \(k ∈ Z^+ \)
(a) show that \(\displaystyle\int^{3k}_k\dfrac{2}{(3x - k)}~dx \) is independent of k
(b) show that \(\displaystyle\int^{2k}_k\dfrac{2}{(2x - k)^2}~dx \) is inversely proportional to k
(a) show that \(\displaystyle\int^{3k}_k\dfrac{2}{(3x - k)}~dx \) is independent of k
[4]
(b) show that \(\displaystyle\int^{2k}_k\dfrac{2}{(2x - k)^2}~dx \) is inversely proportional to k
[3]
[7]
Integration of standard functions

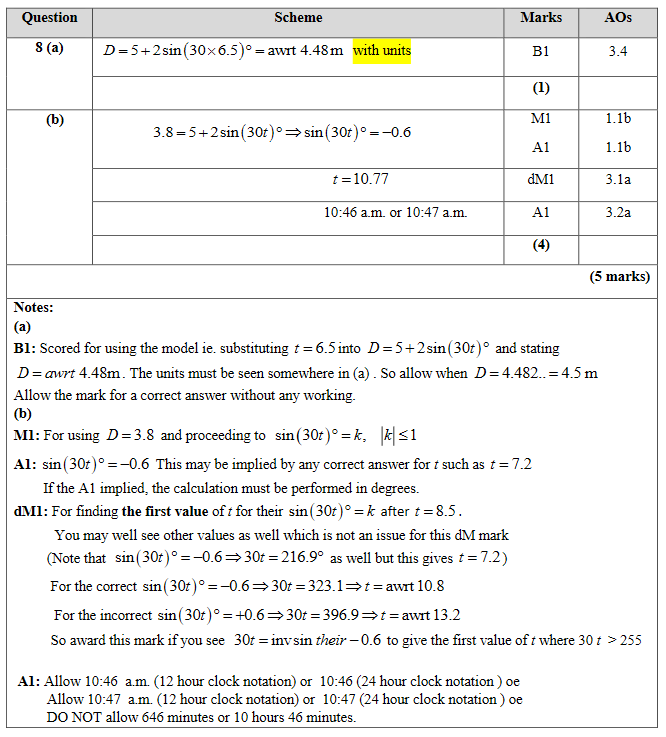
8.
The depth of water, D metres, in a harbour on a particular day is modelled by the formula
\[D=5+2\sin{(30t)}° \qquad 0 ≤ t < 24 \]
where t is the number of hours after midnight.
A boat enters the harbour at 6:30am and it takes 2 hours to load its cargo.
The boat requires the depth of water to be at least 3.8 metres before it can leave the harbour.
(a) Find the depth of the water in the harbour when the boat enters the harbour.
(b) Find, to the nearest minute, the earliest time the boat can leave the harbour.
(Solutions based entirely on graphical or numerical methods are not acceptable.)
\[D=5+2\sin{(30t)}° \qquad 0 ≤ t < 24 \]
where t is the number of hours after midnight.
A boat enters the harbour at 6:30am and it takes 2 hours to load its cargo.
The boat requires the depth of water to be at least 3.8 metres before it can leave the harbour.
(a) Find the depth of the water in the harbour when the boat enters the harbour.
[1]
(b) Find, to the nearest minute, the earliest time the boat can leave the harbour.
(Solutions based entirely on graphical or numerical methods are not acceptable.)
[4]
[5]
Solve problems using trigonometry
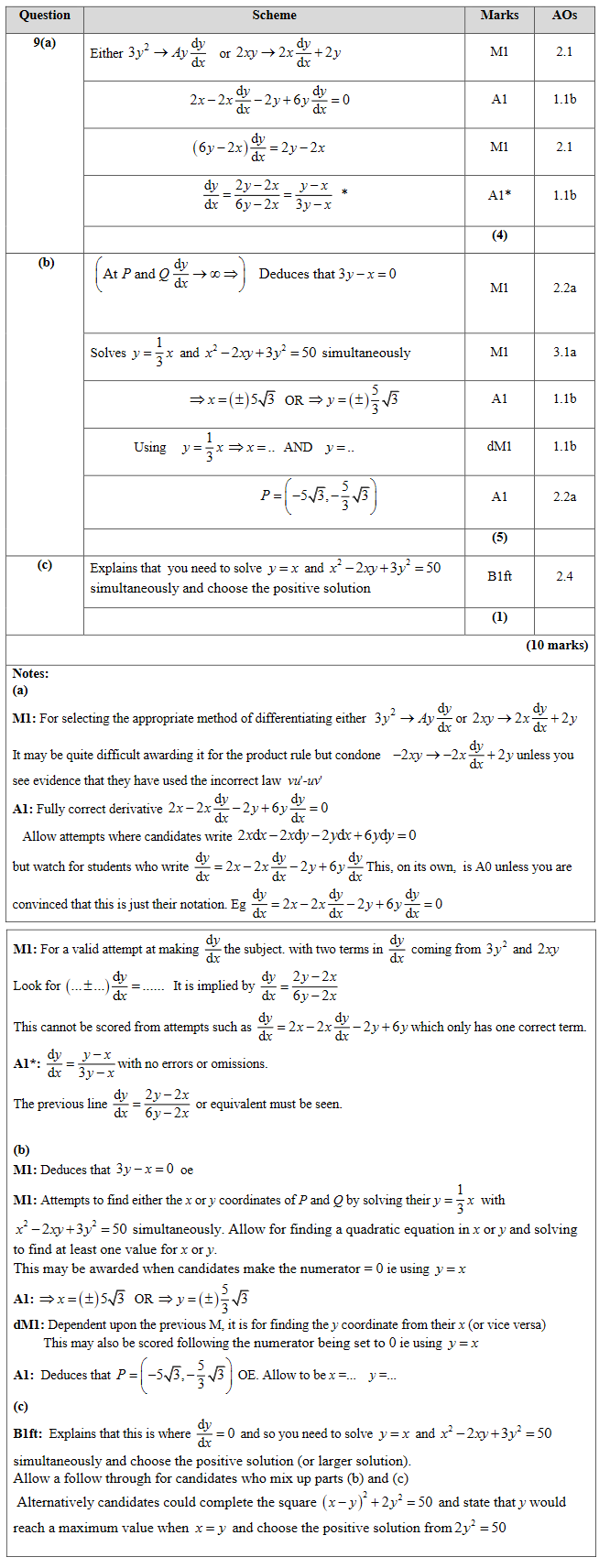
9.

Figure 4 shows a sketch of the curve with equation \(x^2-2xy+3y^2=50\)
(a) Show that \(\dfrac{dy}{dx} = \dfrac{y-x}{3y-x}\)
[4]
The curve is used to model the shape of a cycle track with both x and y measured in km.
The points P and Q represent points that are furthest west and furthest east of the origin O, as shown in Figure 4.
Using part (a),
(b) find the exact coordinates of the point P.
[5]
(c) Explain briefly how to find the coordinates of the point that is furthest north of the origin O. (You do not need to carry out this calculation).
[1]
[10]
Parametric modelling Parametric differentiation
10.
The height above ground, H metres, of a passenger on a roller coaster can be modelled by the differential equation
\[\dfrac{dH}{dt} = \dfrac{H\cos{(0.25t)}}{40} \]
where t is the time, in seconds, from the start of the ride.
Given that the passenger is 5 m above the ground at the start of the ride,
(a) show that \(H = 5e^{0.1\sin{(0.25t)}} \)
(b) State the maximum height of the passenger above the ground.
The passenger reaches the maximum height, for the second time, T seconds after the start of the ride.
(c) Find the value of T.
\[\dfrac{dH}{dt} = \dfrac{H\cos{(0.25t)}}{40} \]
where t is the time, in seconds, from the start of the ride.
Given that the passenger is 5 m above the ground at the start of the ride,
(a) show that \(H = 5e^{0.1\sin{(0.25t)}} \)
[5]
(b) State the maximum height of the passenger above the ground.
[1]
The passenger reaches the maximum height, for the second time, T seconds after the start of the ride.
(c) Find the value of T.
[2]
[8]

11.
(a) Use binomial expansions to show that
\[\sqrt{\dfrac{1+4x}{1-x}} ≈ 1 + \dfrac{5}{2}x - \dfrac{5}{8}x^2 \]
A student substitutes \(x = \dfrac{1}{2}\) into both sides of the approximation shown in part (a) in an attempt to find an approximation to \(\sqrt{6}\)
(b) Give a reason why the student should not use \(x = \dfrac{1}{2}\)
(c) Substitute \(x = \dfrac{1}{11}\) into
\[\sqrt{\dfrac{1+4x}{1-x}} = 1 + \dfrac{5}{2}x - \dfrac{5}{8}x^2 \]
to obtain an approximation to \(\sqrt{6}\). Give your answer as a fraction in its simplest form.
\[\sqrt{\dfrac{1+4x}{1-x}} ≈ 1 + \dfrac{5}{2}x - \dfrac{5}{8}x^2 \]
[6]
A student substitutes \(x = \dfrac{1}{2}\) into both sides of the approximation shown in part (a) in an attempt to find an approximation to \(\sqrt{6}\)
(b) Give a reason why the student should not use \(x = \dfrac{1}{2}\)
[1]
(c) Substitute \(x = \dfrac{1}{11}\) into
\[\sqrt{\dfrac{1+4x}{1-x}} = 1 + \dfrac{5}{2}x - \dfrac{5}{8}x^2 \]
to obtain an approximation to \(\sqrt{6}\). Give your answer as a fraction in its simplest form.
[3]
[10]

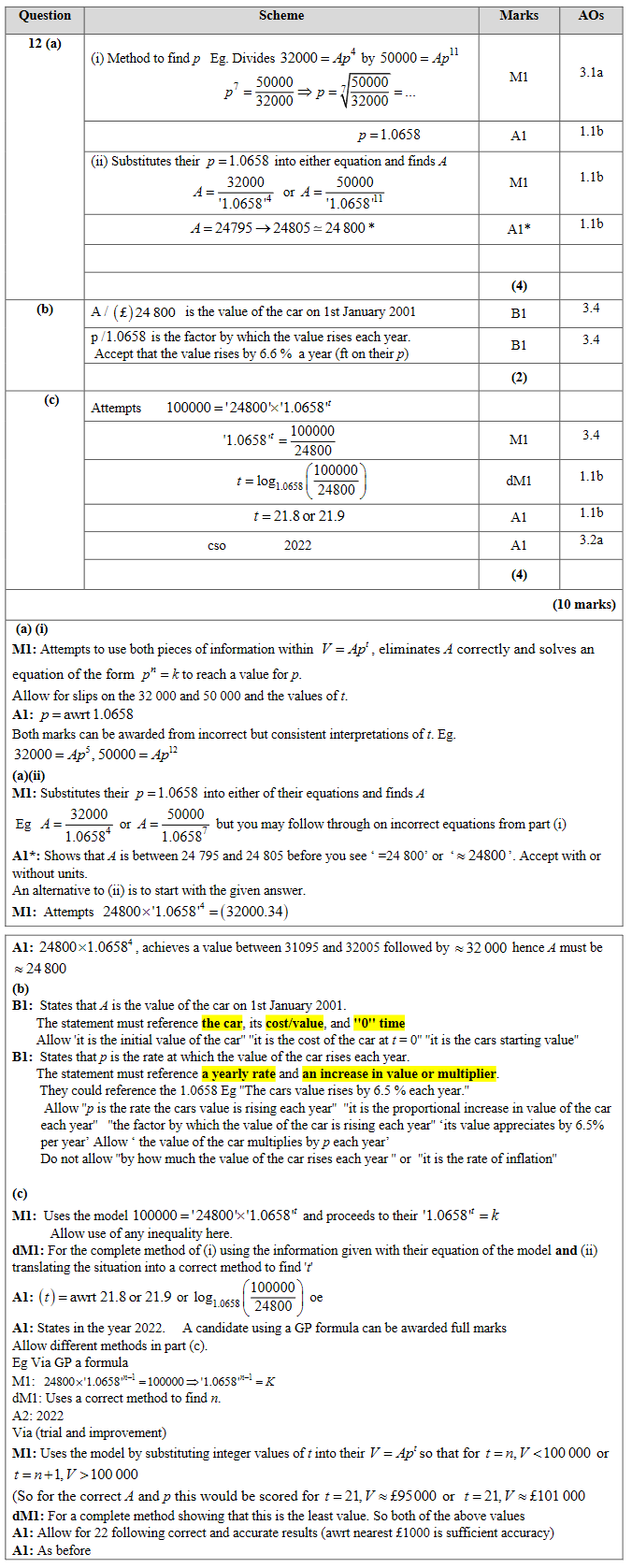
12.
The value, £V, of a vintage car t years after it was first valued on 1st January 2001, is modelled by the equation
\[V = Ap^t \]
where A and p are constants
Given that the value of the car was £32 000 on 1st January 2005 and £50 000 on 1st January 2012
(a) (i) find p to 4 decimal places,
(ii) show that A is approximately 24 800
(b) With reference to the model, interpret
(i) the value of the constant A,
(ii) the value of the constant p.
Using the model,
(c) find the year during which the value of the car first exceeds £100 000
\[V = Ap^t \]
where A and p are constants
Given that the value of the car was £32 000 on 1st January 2005 and £50 000 on 1st January 2012
(a) (i) find p to 4 decimal places,
(ii) show that A is approximately 24 800
[4]
(b) With reference to the model, interpret
(i) the value of the constant A,
(ii) the value of the constant p.
[2]
Using the model,
(c) find the year during which the value of the car first exceeds £100 000
[4]
[10]
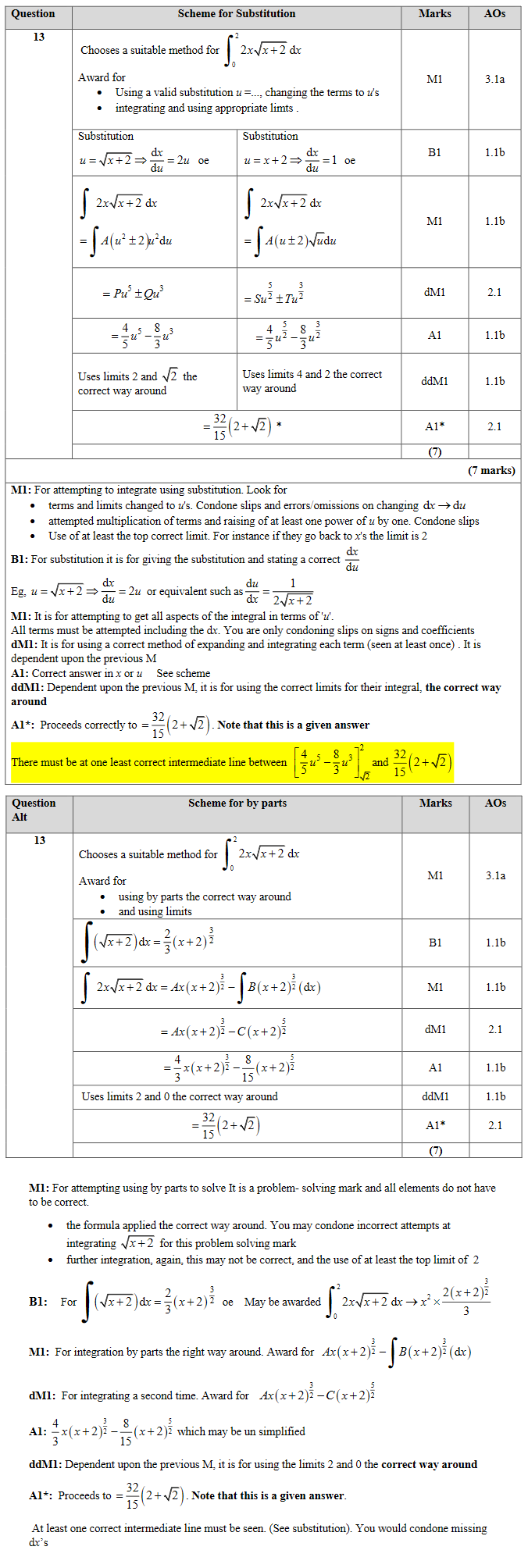
13.
Show that
\[\displaystyle\int^2_0 2x\sqrt{x+2}~ dx = \dfrac{32}{15} \bigg(2 + \sqrt{2}\bigg)\]
\[\displaystyle\int^2_0 2x\sqrt{x+2}~ dx = \dfrac{32}{15} \bigg(2 + \sqrt{2}\bigg)\]
[7]
Integration by substitution Integration by parts
14.
A curve C has parametric equations
\[x=3+2\sin{t}, \quad y=4+2\cos{2t}, \\ 0 ⩽ t < 2π \]
(a) Show that all points on C satisfy \({y=6-(x-3)^2} \)
(b) (i) Sketch the curve C.
(ii) Explain briefly why C does not include all points of \({y=6-(x-3)^2, \quad x∈ℝ} \)
The line with equation \(x+y=k\), where k is a constant, intersects C at two distinct points.
(c) State the range of values of k, writing your answer in set notation.
\[x=3+2\sin{t}, \quad y=4+2\cos{2t}, \\ 0 ⩽ t < 2π \]
(a) Show that all points on C satisfy \({y=6-(x-3)^2} \)
[2]
(b) (i) Sketch the curve C.
(ii) Explain briefly why C does not include all points of \({y=6-(x-3)^2, \quad x∈ℝ} \)
[3]
The line with equation \(x+y=k\), where k is a constant, intersects C at two distinct points.
(c) State the range of values of k, writing your answer in set notation.
[5]
[10]
Discriminant of a quadratic function Parametric equations

END OF QUESTION PAPER
[100]