8.2 Integration of standard functions
General rules
\(\displaystyle\int{f'(x)} dx = f(x) + c \)
\(\displaystyle\int{\dfrac{dy}{dx}} dx = y + c \)
When integrating sums and differences of functions, integrate them separately.
\(\displaystyle\int{\big(f'(x) \pm g'(x)\big)} dx = \displaystyle\int{f'(x)} dx \pm \displaystyle\int{g'(x)} dx\)
When integrating constant multiples of functions, integrate the function and multiply by the constant.
\(\displaystyle\int{kf'(x)} dx = k\displaystyle\int{f'(x)} dx\)
\(\bm{\underline{x^n, \quad n \neq -1}} \)
When integrating \(x^n\) with respect to \(x\), increase the power \(n\) by \(1\), then divide by the new power \(n + 1\).
This works for all rational values of \(n\), i.e. fractions and negative values, except for \(-1\), because division by \(0\) is undefined.
Tip: Take care when increasing negative powers of \(n\) by \(1\), e.g. \(-2+1=-1\) not \(-3\)!
\(\boxed{\displaystyle\int{x^n} dx = \dfrac{x^{n+1}}{n+1} + c, \quad n \neq -1} \)
When integrating a number \(k\) with respect to \(x\), the result is \(kx + c\). Using the above result:
\(\displaystyle\int{k} dx = \displaystyle\int{kx^0} dx = \dfrac{kx^1}{1} + c \)
\(\implies \boxed{\displaystyle\int{k} dx = kx + c} \)
\(\bm{\underline{x^n, n = -1}} \)
\(x^{-1} = \dfrac{1}{x} \)
Exponential functions
Trigonometric functions
Tip: Counterclockwise for integration.
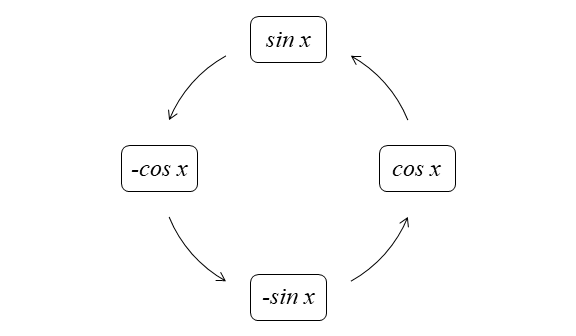
Trigonometric identities can be used to integrate more complex trigonometric functions.
For example, the power reduction formulae can be used to integrate \(\sin^2{x}\) and \(\cos^2{x}\).
\(\displaystyle\int{f'(x)} dx = f(x) + c \)
\(\displaystyle\int{\dfrac{dy}{dx}} dx = y + c \)
When integrating sums and differences of functions, integrate them separately.
\(\displaystyle\int{\big(f'(x) \pm g'(x)\big)} dx = \displaystyle\int{f'(x)} dx \pm \displaystyle\int{g'(x)} dx\)
When integrating constant multiples of functions, integrate the function and multiply by the constant.
\(\displaystyle\int{kf'(x)} dx = k\displaystyle\int{f'(x)} dx\)
\(\bm{\underline{x^n, \quad n \neq -1}} \)
When integrating \(x^n\) with respect to \(x\), increase the power \(n\) by \(1\), then divide by the new power \(n + 1\).
This works for all rational values of \(n\), i.e. fractions and negative values, except for \(-1\), because division by \(0\) is undefined.
Tip: Take care when increasing negative powers of \(n\) by \(1\), e.g. \(-2+1=-1\) not \(-3\)!
\(\boxed{\displaystyle\int{x^n} dx = \dfrac{x^{n+1}}{n+1} + c, \quad n \neq -1} \)
When integrating a number \(k\) with respect to \(x\), the result is \(kx + c\). Using the above result:
\(\displaystyle\int{k} dx = \displaystyle\int{kx^0} dx = \dfrac{kx^1}{1} + c \)
\(\implies \boxed{\displaystyle\int{k} dx = kx + c} \)
\(\bm{\underline{x^n, n = -1}} \)
\(x^{-1} = \dfrac{1}{x} \)
\(\boxed{\displaystyle\int{\dfrac{1}{x}} dx = \ln{x} + c} \)
\(\boxed{\displaystyle\int{\dfrac{1}{kx}} dx = \dfrac{1}{k}\ln{x} + c} \)
Exponential functions
\(\boxed{\displaystyle\int{e^x} dx = e^x + c} \)
\(\boxed{\displaystyle\int{e^{kx}} dx = \dfrac{1}{k}e^{kx} + c} \)
Trigonometric functions
\(\boxed{\displaystyle\int{(\sin{x})} dx = -\cos{x} + c} \)
\(\boxed{\displaystyle\int{(\cos{x})} dx = \sin{x} + c} \)
\(\boxed{\displaystyle\int{(\sec^2{x})} dx = \tan{x} + c} \)
\(\boxed{\displaystyle\int{(\cos{x})} dx = \sin{x} + c} \)
\(\boxed{\displaystyle\int{(\sec^2{x})} dx = \tan{x} + c} \)
\(\boxed{\displaystyle\int{(\sin{kx})} dx = -\dfrac{1}{k}\cos{kx} + c} \)
\(\boxed{\displaystyle\int{(\cos{kx})} dx = \dfrac{1}{k}\sin{kx} + c} \)
\(\boxed{\displaystyle\int{(\sec^2{kx})} dx = \dfrac{1}{k}\tan{kx} + c} \)
\(\boxed{\displaystyle\int{(\cos{kx})} dx = \dfrac{1}{k}\sin{kx} + c} \)
\(\boxed{\displaystyle\int{(\sec^2{kx})} dx = \dfrac{1}{k}\tan{kx} + c} \)
Tip: Counterclockwise for integration.

Trigonometric identities can be used to integrate more complex trigonometric functions.
For example, the power reduction formulae can be used to integrate \(\sin^2{x}\) and \(\cos^2{x}\).
Important
Standard integration results
\(\displaystyle\int{x^n} dx = \dfrac{x^{n+1}}{n+1} + c, \quad n \neq -1 \)
\(\displaystyle\int{\dfrac{1}{kx}} dx = \dfrac{1}{k}\ln{x} + c \)
\(\displaystyle\int{e^{kx}} dx = \dfrac{1}{k}e^{kx} + c \)
\(\displaystyle\int{(\sin{kx})} dx = -\dfrac{1}{k}\cos{kx} + c \)
\(\displaystyle\int{(\cos{kx})} dx = \dfrac{1}{k}\sin{kx} + c \)
\(\displaystyle\int{(\sec^2{kx})} dx = \dfrac{1}{k}\tan{kx} + c \)
\(\displaystyle\int{x^n} dx = \dfrac{x^{n+1}}{n+1} + c, \quad n \neq -1 \)
\(\displaystyle\int{\dfrac{1}{kx}} dx = \dfrac{1}{k}\ln{x} + c \)
\(\displaystyle\int{e^{kx}} dx = \dfrac{1}{k}e^{kx} + c \)
\(\displaystyle\int{(\sin{kx})} dx = -\dfrac{1}{k}\cos{kx} + c \)
\(\displaystyle\int{(\cos{kx})} dx = \dfrac{1}{k}\sin{kx} + c \)
\(\displaystyle\int{(\sec^2{kx})} dx = \dfrac{1}{k}\tan{kx} + c \)
3