Integration is the reverse process of differentiation. The notation for an indefinite integral is:

\(\displaystyle\int{f'(x)} dx = f(x) + c \)

Indefinite integrals always produce a function.

Definite integrals are covered in Topic 8.3.

The constant of integration

Consider the equations below:

\(\textcolor{blue}{y=x^3-2x+2} \quad \textcolor{red}{y=x^{3}-2x} \quad \textcolor{green}{y=x^{3}-2x-2} \)



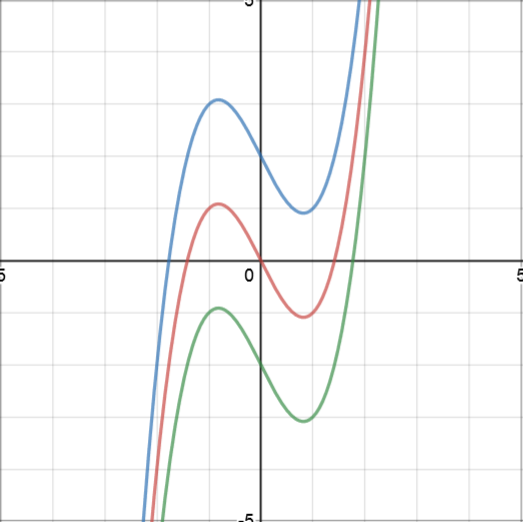
The derivatives of all three equations are the same:

\(\dfrac{dy}{dx} = 3x^2-2 \)

So when performing the reverse process (integration), it is impossible to know which equation was the starting point.

A constant of integration (\(\bm{c}\)) is required to represent the \(y\)-intercept. Hence:

\(\displaystyle\int{(3x^2-2)} dx = x^3-2x + \bm{c} \)

\(\implies y=x^3-2x+c\)

If you know a point that the original equation goes through, then you can substitute the \(x\) and \(y\)-coordinates into the equation and solve for \(c\).