3.2 Circles
Equations of circles
There are 2 forms for the equation of a circle.
The "completed square" form
Multiply out both brackets and rearrange to convert to the "multiplied out" form.
The "multiplied out" form
Complete the square for both \(x\) and \(y\) to convert to the "completed square" form.
Straight lines and circles
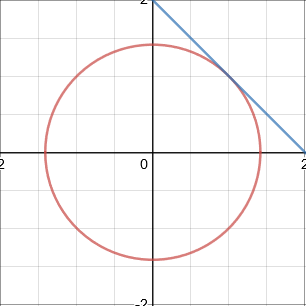
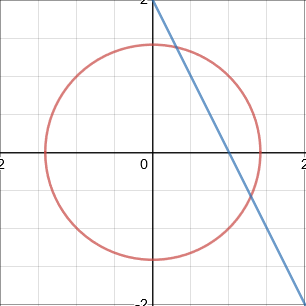
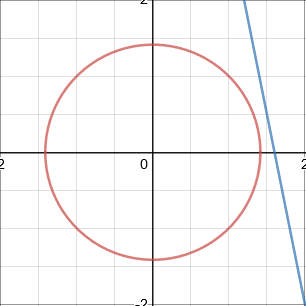
A straight line can intersect a circle once, twice, or not at all.
If a straight line intersects a circle once, by touching it, then it also a tangent of the circle.
Properties of circles
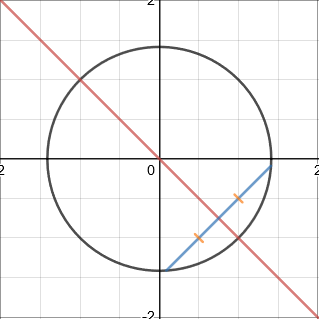
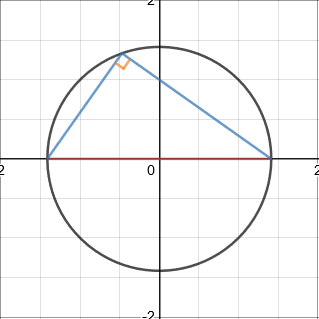
With these properties, the equation of a circumcircle of a triangle with given vertices and the equation of a tangent at a specified point on the circumference can be found.
There are 2 forms for the equation of a circle.
The "completed square" form
\((x-a)^2+(y-b)^2=r^2\)
where \(r\) is the radius and \((a,b)\) is the centre of the circle.
Multiply out both brackets and rearrange to convert to the "multiplied out" form.
The "multiplied out" form
\(x^2+y^2-2px-2qy+s=0\)
where \(\sqrt{p^2+q^2-s}\) is the radius and \((p,q)\) is the centre of the circle.
Complete the square for both \(x\) and \(y\) to convert to the "completed square" form.
Straight lines and circles
A straight line can intersect a circle once, twice, or not at all.
If a straight line intersects a circle once, by touching it, then it also a tangent of the circle.

Intersect once (tangent)

Intersect twice

Does not intersect
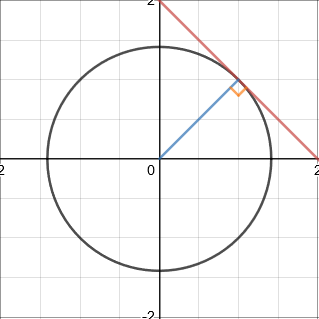
Properties of circles

A tangent to a circle is perpendicular to the radius of the circle at the point of intersection.

The perpendicular bisector of a chord will go through the centre of a circle.

The angle in a semicircle is a right angle.
With these properties, the equation of a circumcircle of a triangle with given vertices and the equation of a tangent at a specified point on the circumference can be found.
Important
There are 2 forms for the equation of a circle:
- \((x-a)^2+(y-b)^2=r^2\), radius is \(r\) and center is \((a,b)\)
- \(x^2+y^2-2px-2qy+s=0\), radius is \(\sqrt{p^2+q^2-s}\) and center is \((p,q)\)
3