7.5 Turning points
Stationary points
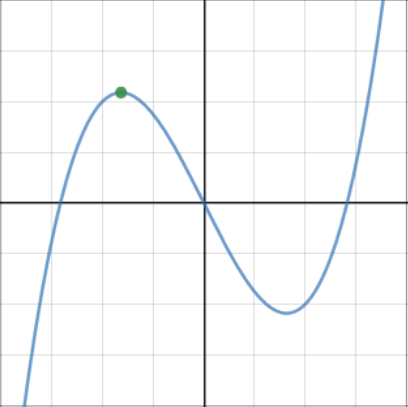
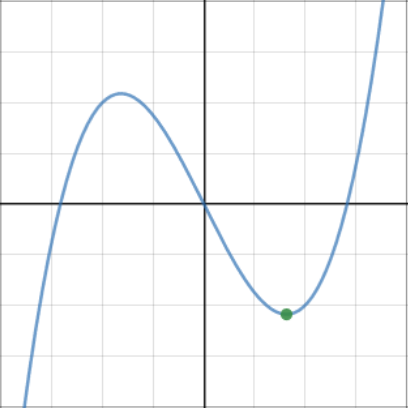
Stationary points occur when \(\dfrac{dy}{dx}=0\). The second derivative can be used to test whether the stationary point is a maximum or a minimuum.
Points of inflection
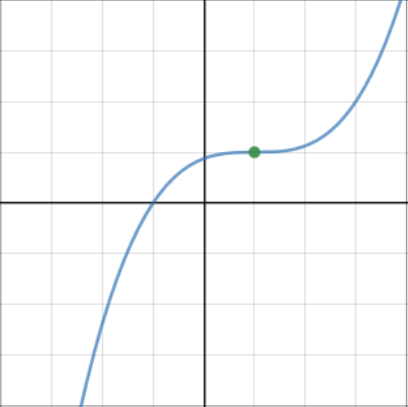
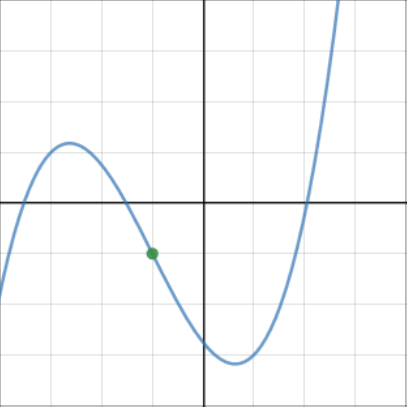
Points of inflection occur when \(\dfrac{d^2y}{dx^2} = 0\). Points of inflections can be stationary or non-stationary.
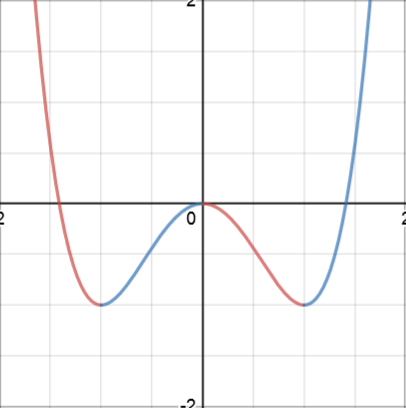
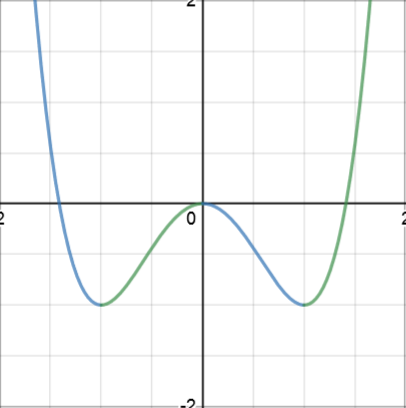
Decreasing or increasing functions
Sections of curves can be decreasing or increasing.
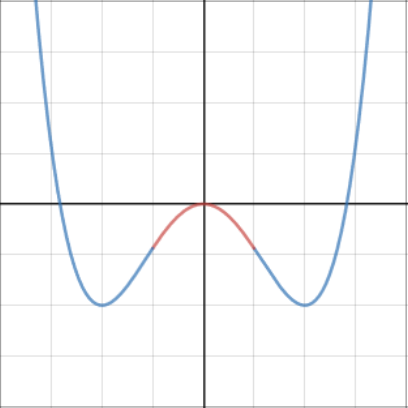
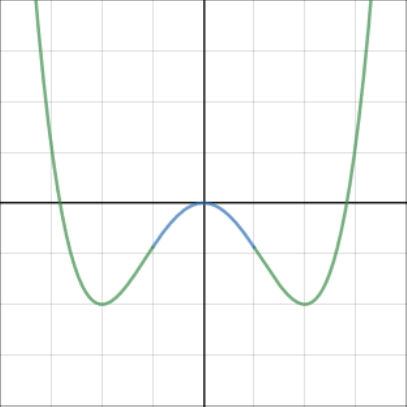
Concave or convex
Sections of curves can be concave (n-shaped, imagine the entrance of a cave) or convex (u-shaped).
Stationary points occur when \(\dfrac{dy}{dx}=0\). The second derivative can be used to test whether the stationary point is a maximum or a minimuum.
Maximum points have \(\dfrac{dy}{dx}=0\) and \(\dfrac{d^2y}{dx^2} < 0\).

Minimum points have \(\dfrac{dy}{dx}=0\) and \(\dfrac{d^2y}{dx^2} > 0\).

Points of inflection
Points of inflection occur when \(\dfrac{d^2y}{dx^2} = 0\). Points of inflections can be stationary or non-stationary.
Stationary points of inflection have \(\dfrac{dy}{dx}=0\) and \(\dfrac{d^2y}{dx^2} = 0\).

Non-stationary points of inflection have \(\dfrac{dy}{dx} \neq 0\) and \(\dfrac{d^2y}{dx^2} = 0\).

Decreasing or increasing functions
Sections of curves can be decreasing or increasing.
Decreasing sections of curves have \(\dfrac{dy}{dx} < 0\).

Increasing sections of curves have \(\dfrac{dy}{dx} > 0\).

Concave or convex
Sections of curves can be concave (n-shaped, imagine the entrance of a cave) or convex (u-shaped).
Concave sections of curves have \(\dfrac{d^2y}{dx^2} < 0\).

Convex sections of curves have \(\dfrac{d^2y}{dx^2} > 0\).

Important
Stationary points occur when \(\dfrac{dy}{dx}=0\).
Maximum points have \(\dfrac{dy}{dx}=0\) and \(\dfrac{d^2y}{dx^2} < 0\).
Minimum points have \(\dfrac{dy}{dx}=0\) and \(\dfrac{d^2y}{dx^2} > 0\).
Stationary points of inflection have \(\dfrac{dy}{dx}=0\) and \(\dfrac{d^2y}{dx^2} = 0\).
Non-stationary points of inflection have \(\dfrac{dy}{dx} \neq 0\) and \(\dfrac{d^2y}{dx^2} = 0\).
Decreasing sections of curves have \(\dfrac{dy}{dx} < 0\) and increasing sections of curves have \(\dfrac{dy}{dx} > 0\).
Concave sections of curves have \(\dfrac{d^2y}{dx^2} < 0\) and convex sections of curves have \(\dfrac{d^2y}{dx^2} > 0\).
Maximum points have \(\dfrac{dy}{dx}=0\) and \(\dfrac{d^2y}{dx^2} < 0\).
Minimum points have \(\dfrac{dy}{dx}=0\) and \(\dfrac{d^2y}{dx^2} > 0\).
Stationary points of inflection have \(\dfrac{dy}{dx}=0\) and \(\dfrac{d^2y}{dx^2} = 0\).
Non-stationary points of inflection have \(\dfrac{dy}{dx} \neq 0\) and \(\dfrac{d^2y}{dx^2} = 0\).
Decreasing sections of curves have \(\dfrac{dy}{dx} < 0\) and increasing sections of curves have \(\dfrac{dy}{dx} > 0\).
Concave sections of curves have \(\dfrac{d^2y}{dx^2} < 0\) and convex sections of curves have \(\dfrac{d^2y}{dx^2} > 0\).
3