9.2 Iterative methods
Iterative methods can be used to solve equations which are otherwise difficult or impossible to solve.
To solve an equation of the form \(f(x) = 0\) using an iterative method, rearrange \(f(x) = 0 \) into the form \(x = g(x) \) and use the iterative formula \(x_{n+1} = g(x_n) \).
Converging iterations
Some iterations will converge to a root. If this happens from the same direction, the representation on a graph is known as a staircase diagram.
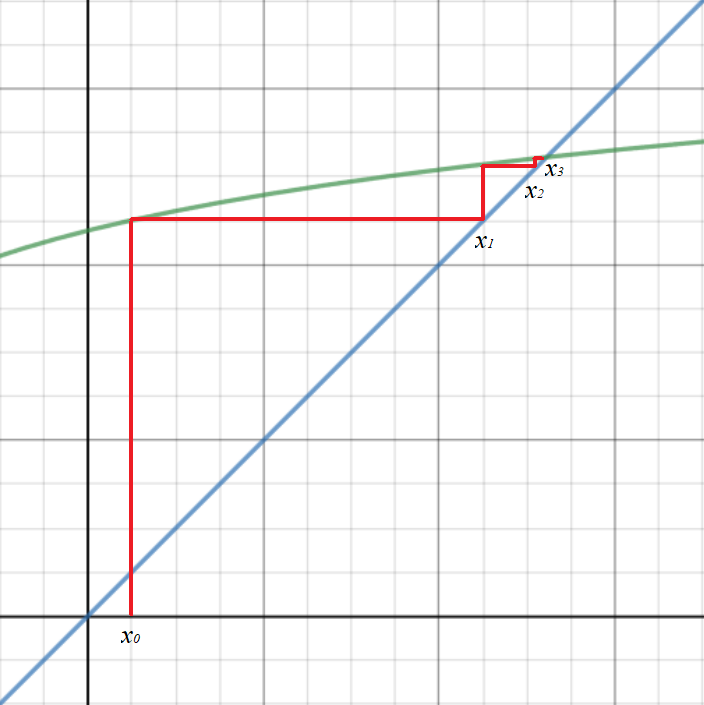
If this happens by alternating above and below the root, the representation on a graph is known as a cobweb diagram.
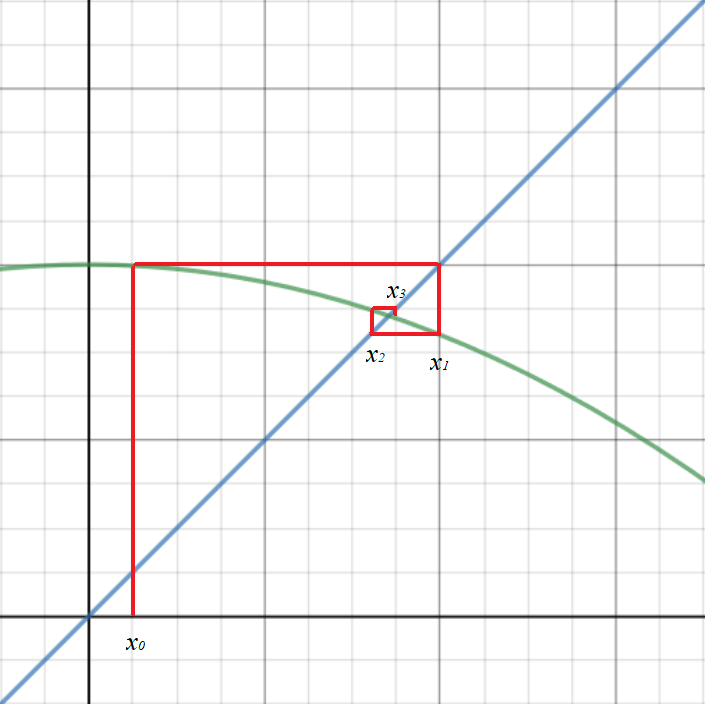
Diverging iterations
Not iterations converge to a root. Sometimes, iterations can diverge away from the root. In this case, it will be impossible to obtain a solution for the root.
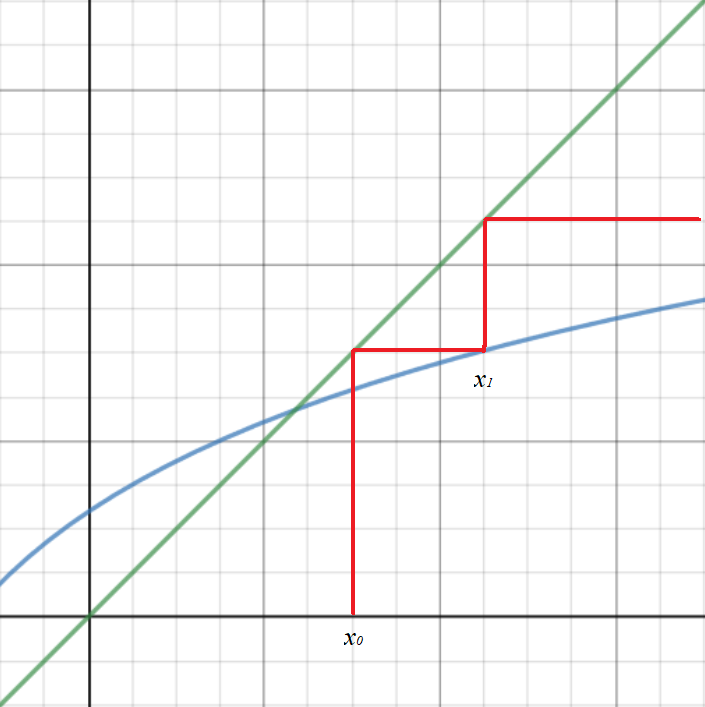
To solve an equation of the form \(f(x) = 0\) using an iterative method, rearrange \(f(x) = 0 \) into the form \(x = g(x) \) and use the iterative formula \(x_{n+1} = g(x_n) \).
Converging iterations
Some iterations will converge to a root. If this happens from the same direction, the representation on a graph is known as a staircase diagram.

If this happens by alternating above and below the root, the representation on a graph is known as a cobweb diagram.

Diverging iterations
Not iterations converge to a root. Sometimes, iterations can diverge away from the root. In this case, it will be impossible to obtain a solution for the root.

Important
Iterative methods
To solve an equation of the form \(f(x) = 0\) using an iterative method, rearrange \(f(x) = 0 \) into the form \(x = g(x) \) and use the iterative formula \(x_{n+1} = g(x_n) \).
To solve an equation of the form \(f(x) = 0\) using an iterative method, rearrange \(f(x) = 0 \) into the form \(x = g(x) \) and use the iterative formula \(x_{n+1} = g(x_n) \).
3