9.1 Locating roots by considering changes of sign
Roots of \(f(x) = 0\) can be located by considering changes of sign of \(f(x)\) in an interval of \(x\) on which \(f(x)\) is sufficiently well behaved.
If the function \(f(x)\) is continuous on the small interval \([a,b]\) and \(f(a)\) and \(f(b)\) have opposite signs, then \(f(x)\) has at least one root, \(x\), in the interval \(a < x < b\).
For example, in the graph below of \(y = f(x)\), we can see that there is one root between \(0\) and \(1\), because \(f(0) < 0 \) and \(f(1) > 0 \).
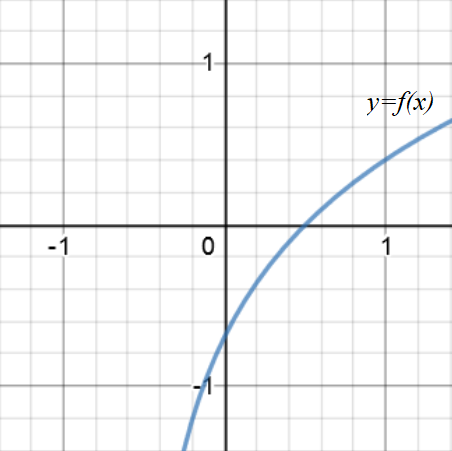
Limitations of this method
A change of sign does not necessarily mean there is only one root, as demonstrated below.
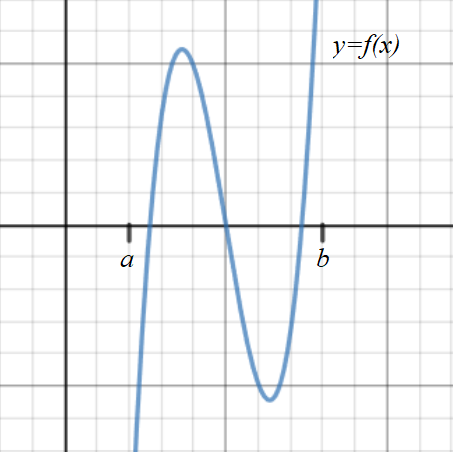
For example, in the graph below of \(y = f(x)\), we can see that there are multiple roots between \(a\) and \(b\). This happens when there are an odd number of roots in the interval.
Alternatively, despite there being a sign change, there is no root in the example below, because the graph is discontinuous between \(a\) and \(b\) due to the asymptote.
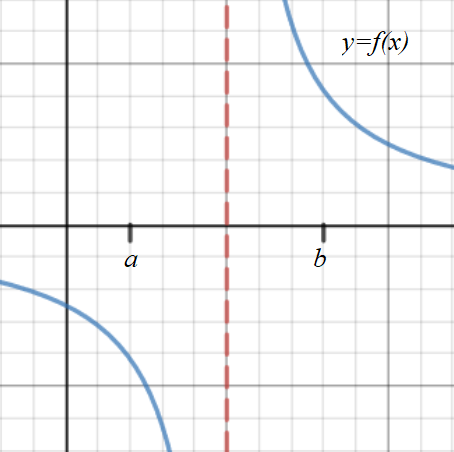
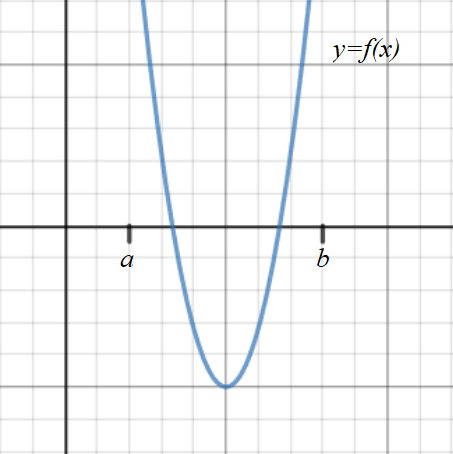
Sometimes, there are roots even though there is no sign change. This happens when the interval is too large and there are an even number of roots in the interval.
If the function \(f(x)\) is continuous on the small interval \([a,b]\) and \(f(a)\) and \(f(b)\) have opposite signs, then \(f(x)\) has at least one root, \(x\), in the interval \(a < x < b\).
For example, in the graph below of \(y = f(x)\), we can see that there is one root between \(0\) and \(1\), because \(f(0) < 0 \) and \(f(1) > 0 \).
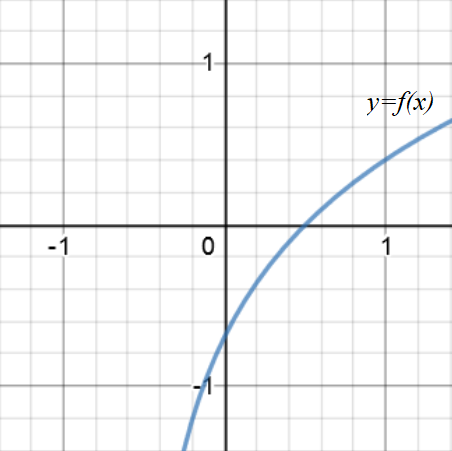
Limitations of this method
A change of sign does not necessarily mean there is only one root, as demonstrated below.
For example, in the graph below of \(y = f(x)\), we can see that there are multiple roots between \(a\) and \(b\). This happens when there are an odd number of roots in the interval.

Alternatively, despite there being a sign change, there is no root in the example below, because the graph is discontinuous between \(a\) and \(b\) due to the asymptote.
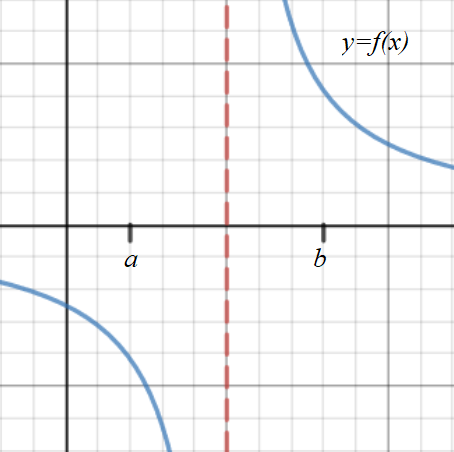
Sometimes, there are roots even though there is no sign change. This happens when the interval is too large and there are an even number of roots in the interval.

Important
Locating roots by considering changes of sign
If the function \(f(x)\) is continuous on the interval \([a,b]\) and \(f(a)\) and \(f(b)\) have opposite signs, then \(f(x)\) has at least one root, \(x\), in the interval \(a < x < b\).
If the function \(f(x)\) is continuous on the interval \([a,b]\) and \(f(a)\) and \(f(b)\) have opposite signs, then \(f(x)\) has at least one root, \(x\), in the interval \(a < x < b\).
3