A-Level Maths Edexcel 9MA0
Paper 2 - Jun 2018 9MA0/02
Time allowed: 2 h 0 min.
The total mark for this paper is 100.
The marks for each question are shown in brackets [ ].
(a) Find \(gg(5)\).
(b) State the range of \(g\).
(c) Find \(g^{-1}(x) \), stating its domain.
Composite functions Inverse functions Functions, mappings, domain and range

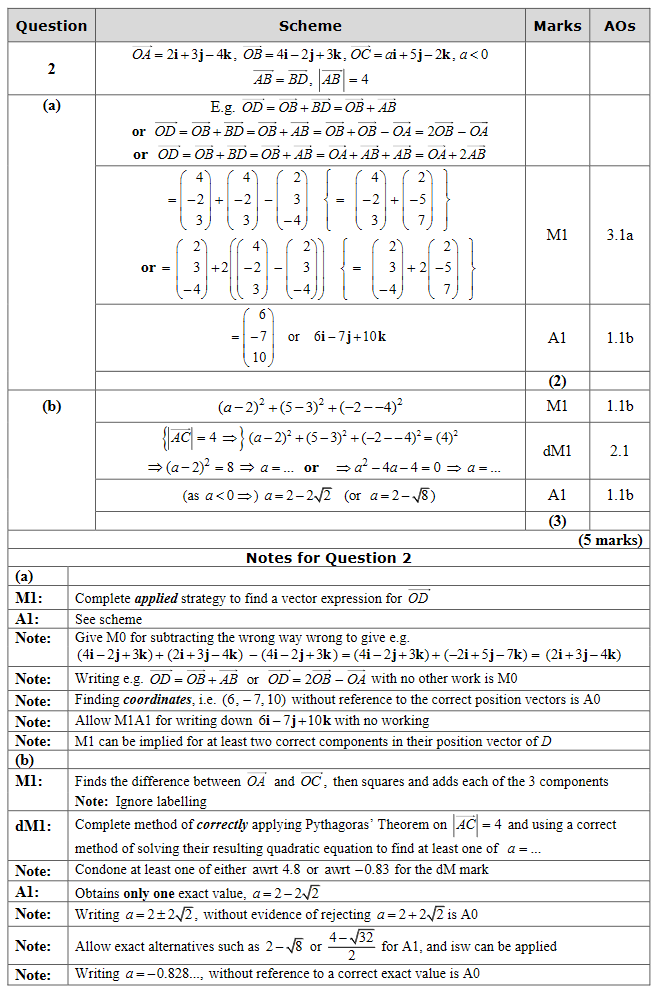
the point A has position vector \((2\bold{i}+3\bold{j}-4\bold{k})\),
the point B has position vector \((4\bold{i}-2\bold{j}+3\bold{k})\),
and the point C has position vector \((a\bold{i}+5\bold{j}-2\bold{k})\), where a is a constant and \({a < 0}\)
D is the point such that \(\overrightarrow{AB} = \overrightarrow{BD} \).
(a) Find the position vector of D.
Given \(|\overrightarrow{AC}| = 4\)
(b) find the value of a.
Magnitude and direction of a vector Position vectors
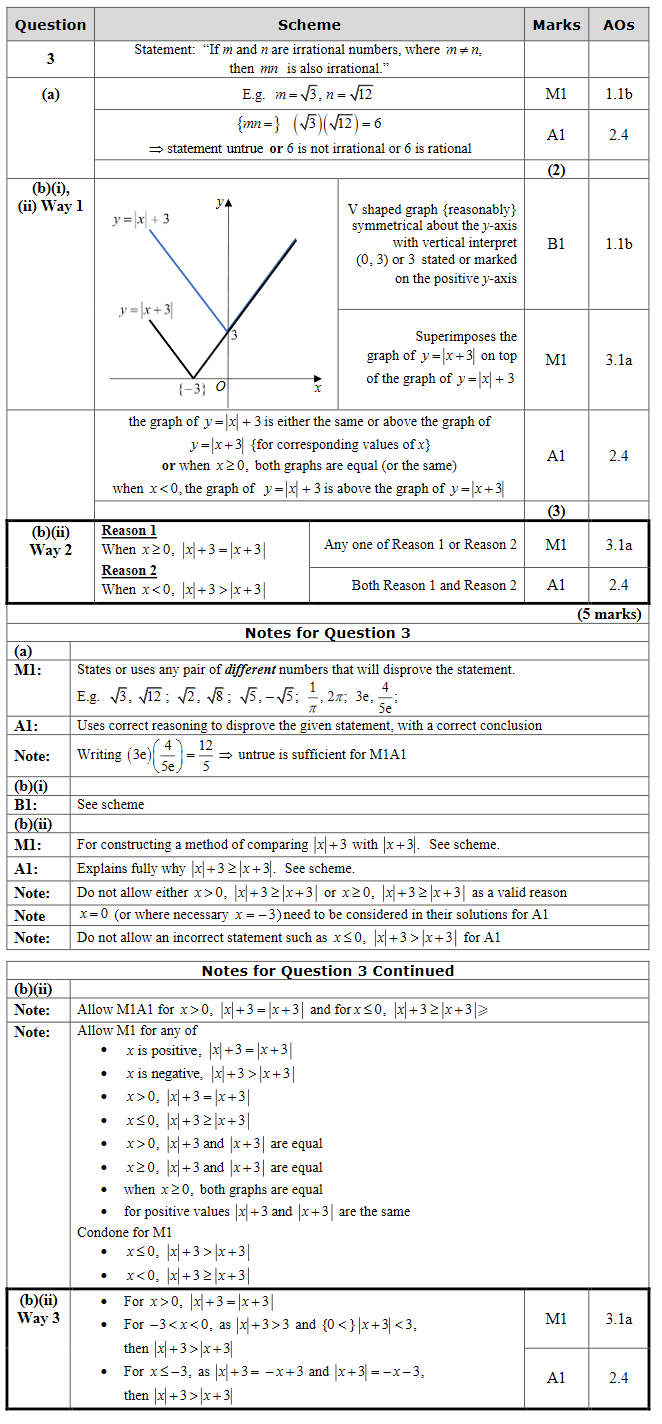
Disprove this statement by means of a counter example.
(b) (i) Sketch the graph of \(y=|x|+3\)
(ii) Explain why \(|x|+3 ⩾ |x+3|\) for all real values of x.
Disproof by counter example Modulus
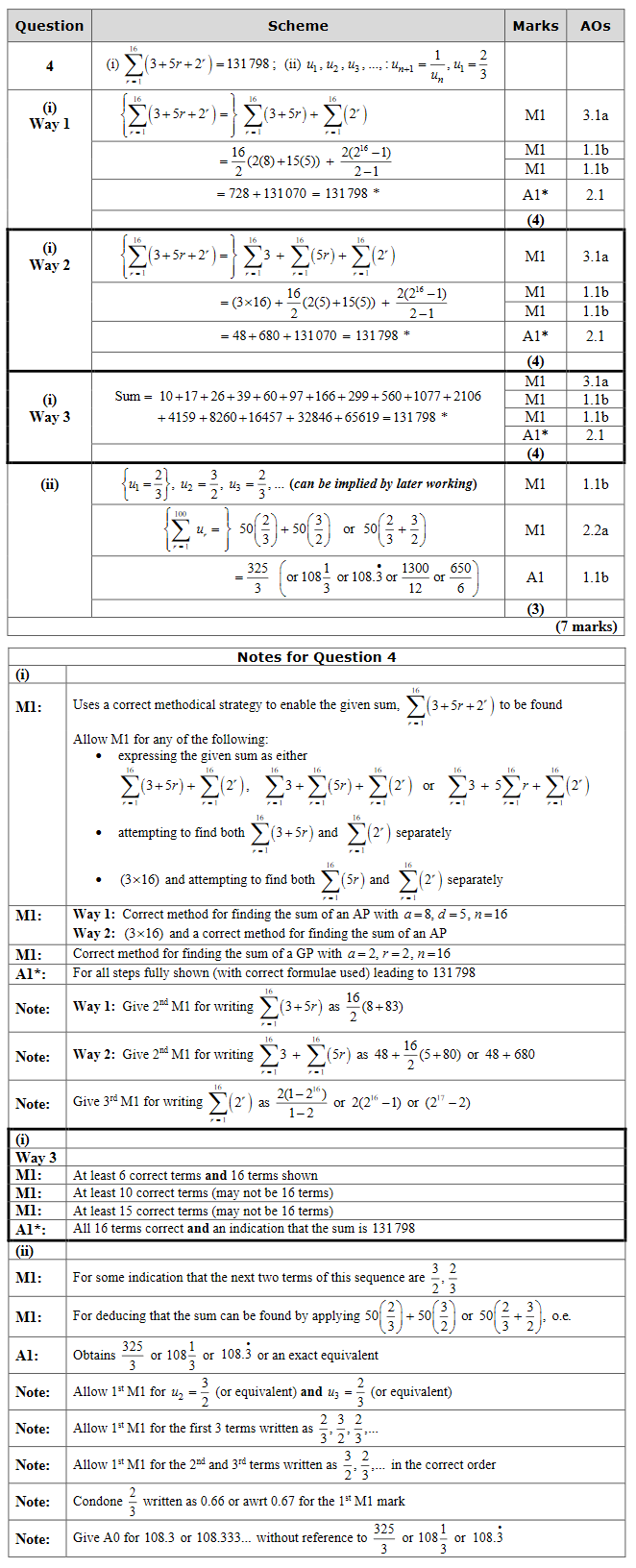
\[\displaystyle\sum^{16}_{r=1} (3 + 5r + 2^r) = 131 798 \]
(ii) A sequence \(u_1, u_2, u_3, ... \) is defined by
\[ u_{n+1} = \dfrac{1}{u_n}, \qquad u_1 = \dfrac{2}{3} \]
Find the exact value of \(\displaystyle\sum^{100}_{r=1} u_r \)
Sequences Sigma notation Arithmetic sequences and series Geometric sequences and series
(a) Show that, for this equation, the Newton-Raphson formula can be written
\[x_{n+1} = \dfrac{4x_n^3 + x_n^2 + 1}{6x_n^2 + 2x_n} \]
Using the formula given in part (a) with \(x_1=1\)
(b) find the values of \(x_2\) and \(x_3\)
(c) Explain why, for this question, the Newton-Raphson method cannot be used with \({x_1=0}\)

(a) (i) Calculate \(f(2)\)
(ii) Write \(f(x)\) as a product of two algebraic factors.
Using the answer to (a)(ii),
(b) prove that there are exactly two real solutions to the equation
\[-3y^6+8y^4-9y^2+10=0 \]
(c) deduce the number of real solutions, for \({7π⩽θ<10π}\), to the equation
\[3\tan^3{θ}-8\tan^2{θ}+9\tan{θ}-10=0\]
Discriminant of a quadratic function Polynomials Factor theorem Solve trigonometric equations

\[4\sin{x} = \sec{x} \]
(ii) Solve, for \({0⩽x⩽360°}\), the equation
\[5\sin{θ} - 5\cos{θ} = 2 \]
giving your answers to one decimal place.
(Solutions based entirely on graphical or numerical methods are not acceptable.)
a cosθ + b sinθ Solve trigonometric equations
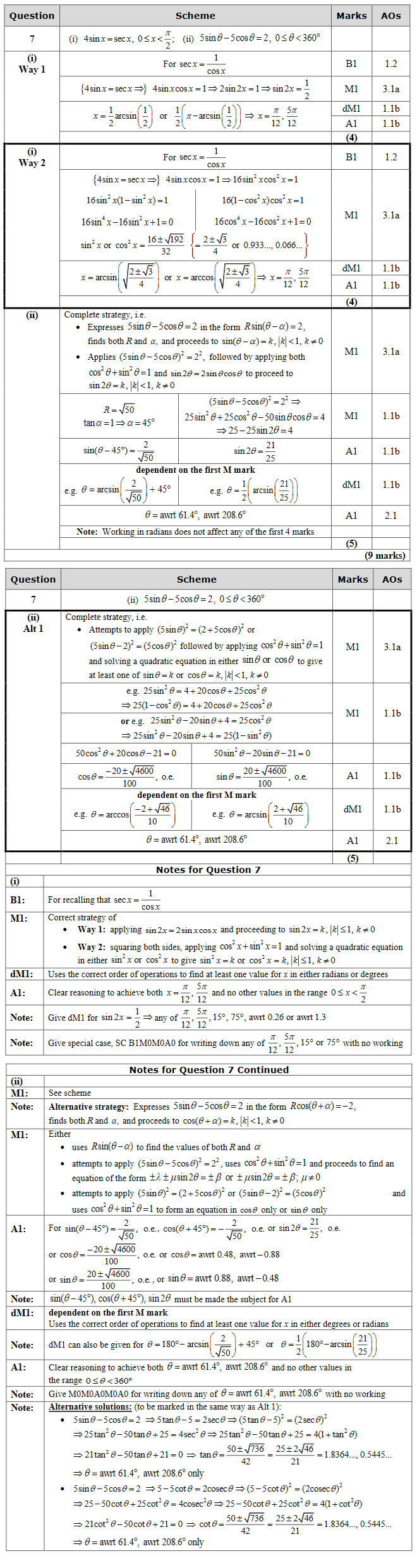
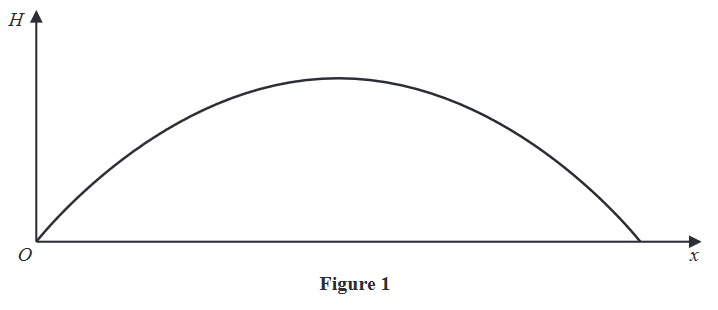
Figure 1 is a graph showing the trajectory of a rugby ball.
The height of the ball above the ground, H metres, has been plotted against the horizontal distance, x metres, measured from the point where the ball was kicked.
The ball travels in a vertical plane.
The ball reaches a maximum height of 12 metres and hits the ground at a point 40 metres from where it was kicked.
(a) Find a quadratic equation linking H with x that models this situation.
The ball passes over the horizontal bar of a set of rugby posts that is perpendicular to the path of the ball. The bar is 3 metres above the ground.
(b) Use your equation to find the greatest horizontal distance of the bar from O.
(c) Give one limitation of the model.
Quadratic functions and graphs Use of functions in modelling
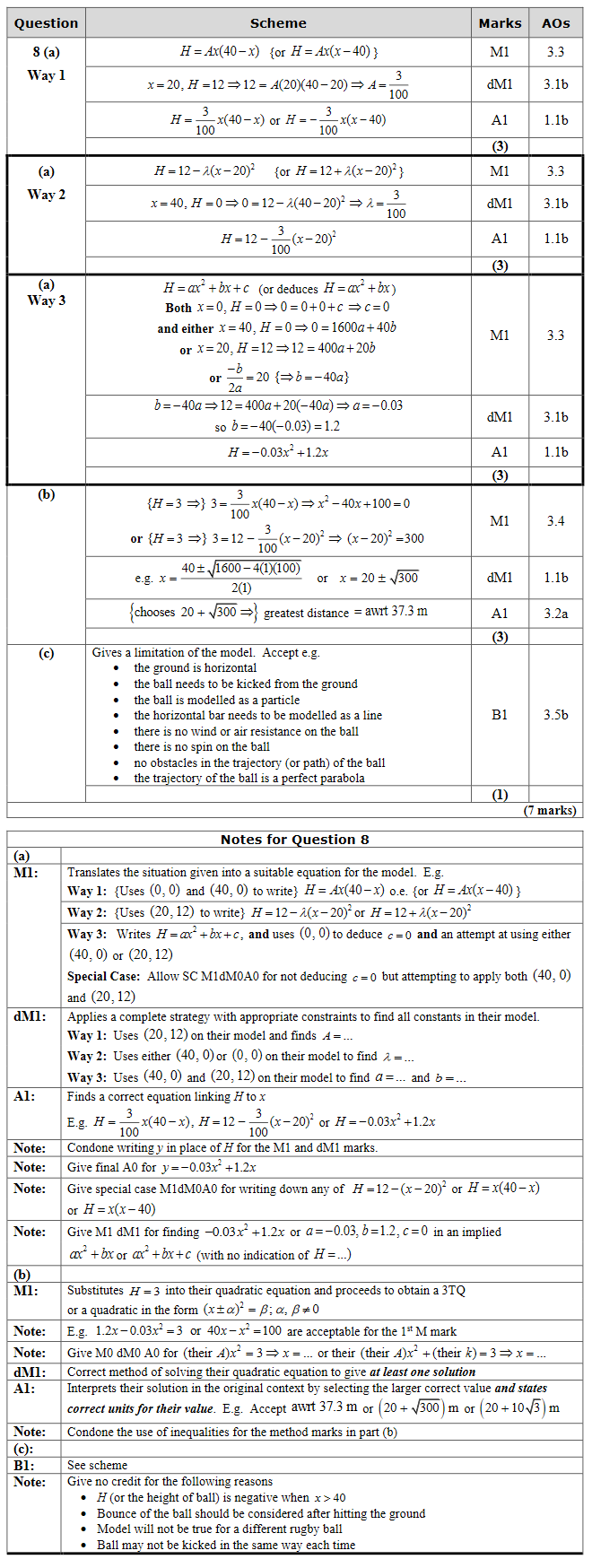
\[\dfrac{d}{dθ}(\cos{}) = -\sin{θ} \]
You may assume the formula for \(\cos{(A±B)}\) and that as \({h→0}\), \(\dfrac{\sin{h}}{h} → 1 \) and \(\dfrac{\cos{h} - 1}{h} → 0 \)
Differentiation from first principles

Four minutes later, the radius of the mint is 3 mm.
In a simple model, the rate of decrease of the radius of the mint is inversely proportional to the square of the radius.
Using this model and all the information given,
(a) find an equation linking the radius of the mint and the time.
(You should define the variables that you use.)
(b) Hence find the total time taken for the mint to completely dissolve. Give your answer in minutes and seconds to the nearest second.
(c) Suggest a limitation of the model.
Differential equations Solve differential equations
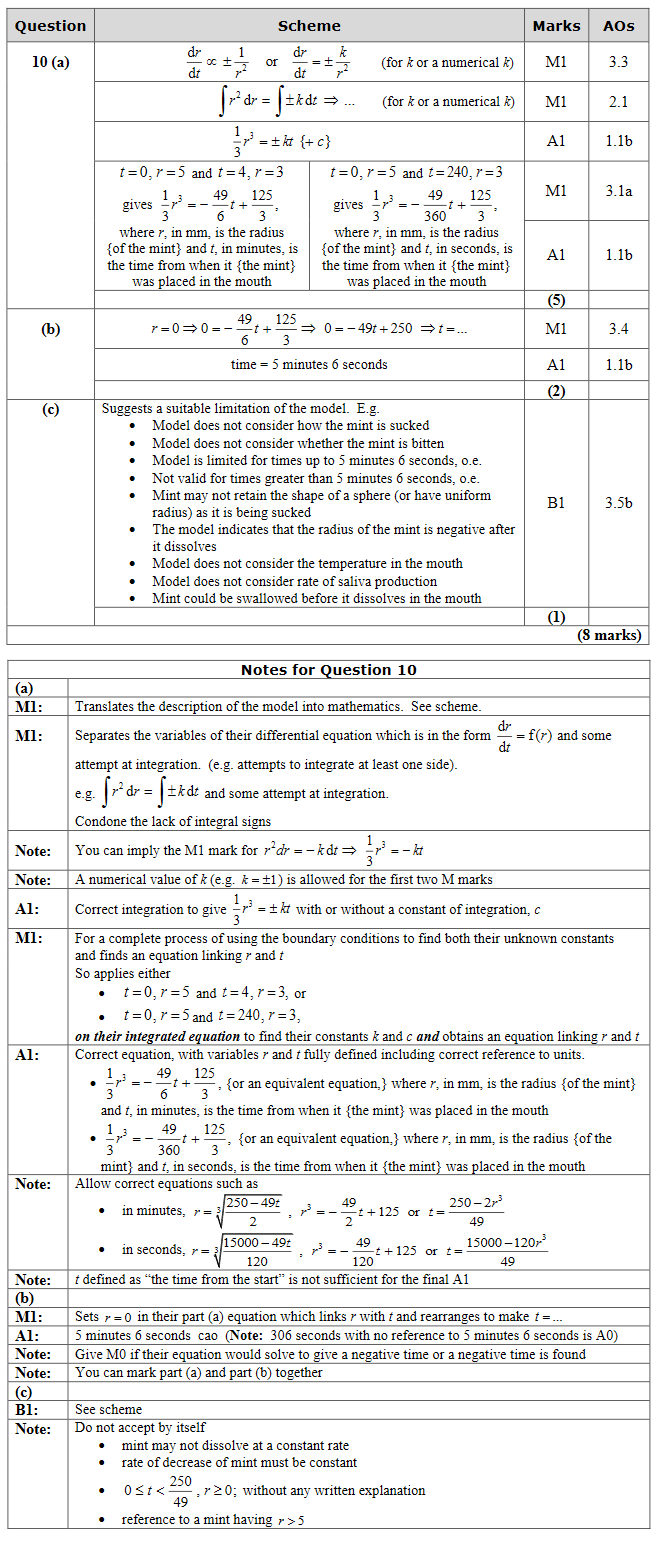
(a) Find the values of the constants A, B and C.
\[f(x) = \dfrac{1+11x-6x^2}{(x-3)(1-2x)}, \qquad x > 3\]
(b) Prove that \(f(x)\) is a decreasing function.
Partial fractions Differentiation of standard functions Turning points

\[1-\cos{2θ} ≡ \tan{θ}\sin{2θ}, \]\[θ ≠ \dfrac{(2n+1)π}{2}, \qquad n∈Z\]
(b) Hence solve, for \({-\dfrac{π}{2} < x < \dfrac{π}{2}} \), the equation
\[(\sec^2{x}-5)(1-\cos{2x}) = 3\tan^2{x}\sin{2x} \]
Give any non-exact answer to 3 decimal places where appropriate.
Solve trigonometric equations Proofs involving trigonometry
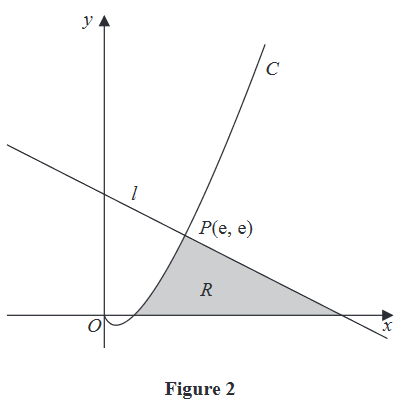
Figure 2 shows a sketch of part of the curve C with equation
\[y = x\ln{x}, \qquad x > 0\]
The line l is the normal to C at the point \(P(e, e)\)
The region R, shown shaded in Figure 2, is bounded by the curve C, the line l and the x-axis.
Show that the exact area of R is \(Ae^2+B\) where A and B are rational numbers to be found.
Straight lines Area under and between curves Integration by parts
The number of mice, N, in the population, t months after the start of the study, is modelled by the equation
\[N = \dfrac{900}{3+7e^{-0.25t}},\]\[t∈ℝ, \qquad t⩾0\]
(a) Find the number of mice in the population at the start of the study.
(b) Show that the rate of growth \(\dfrac{dN}{dt}\) is given by \({\dfrac{dN}{dt} = \dfrac{N(300-N)}{1200}}\)
The rate of growth is a maximum after T months.
(c) Find, according to the model, the value of T.
According to the model, the maximum number of mice on the island is P.
(d) State the value of P.
Exponential modelling Quotient rule
