Consider the graph below, where A is \((x, x+h)\) and B is \((f(x), f(x+h))\).



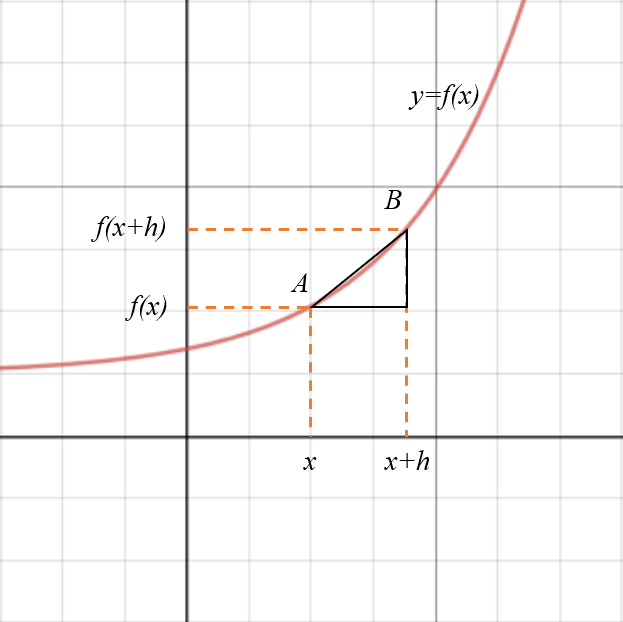
The gradient of the line segment \(AB\) is \(\dfrac{f(x+h) - f(x)}{x+h - x} \implies \dfrac{f(x+h) - f(x)}{h} \).

As the value of \(h\) decreases, the gradient of \(AB\) approaches the gradient \(f'(x)\) of the tangent at \(A\).

This can be expressed as a limit:

\(\boxed{f'(x) = \lim\limits_{h→0} \Big(\dfrac{f(x+h) - f(x)}{h} \Big)}\)

This is known as differentiation from first principles.