Area under curves

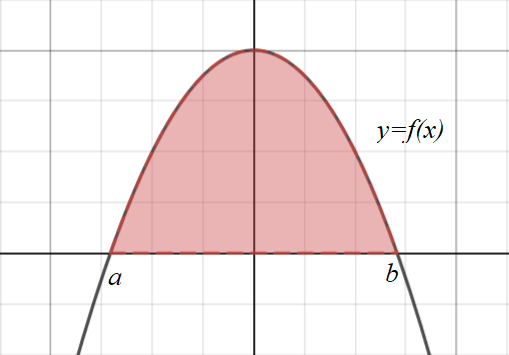
Definite integrals can be used to calculate the area between a curve and the \(x\) axis.

\(Area = \displaystyle\int_a^b{f(x)} dx \)



Area between lines and curves

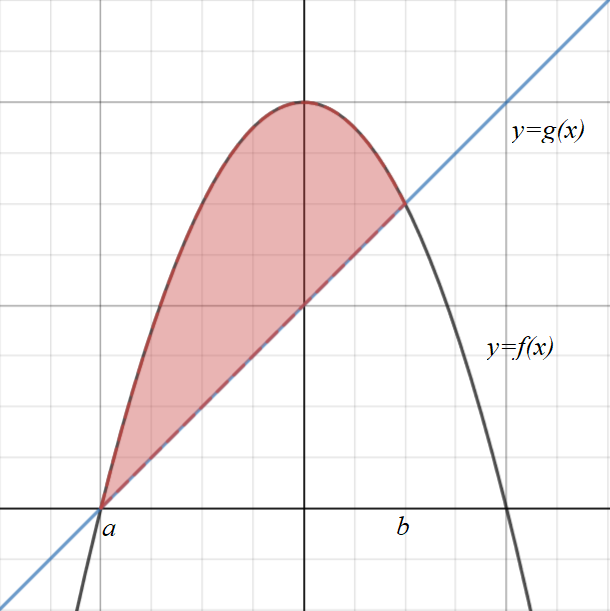
The area between lines and curves can be found by subtracting the one which is "under" the area from the one which is "above" the area.

In the example below, the curve is "above" the area and the line is "below" the area.

\(Area = \displaystyle\int_a^b{\big(f(x) - g(x)\big)} dx \)



Area between curves

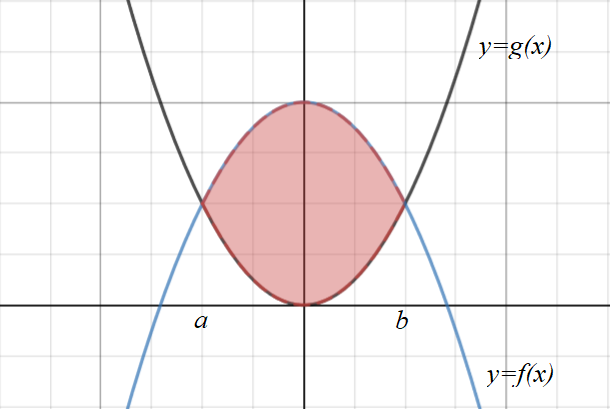
The same applies for area between curves.

\(Area = \displaystyle\int_a^b{\big(f(x) - g(x)\big)} dx \)



Area under the \(\bm{\underline{x}}\)-axis

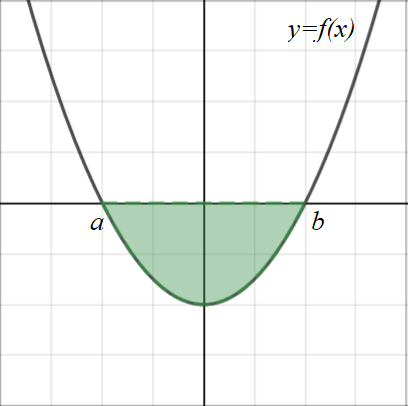
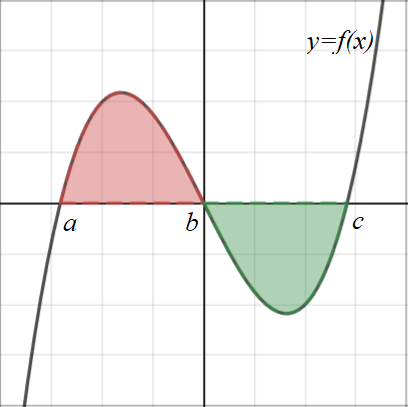
When the area is under the \(x\)-axis, the definite integral will return a negative number. Obviously, areas can't be negative, so use the positive value for the area.

\(Area = \bigg|\displaystyle\int_a^b{f(x)} dx\bigg| \)



Tip: When the area consists of areas above and below the \(x\)-axis, the definite integral needs to be split and the areas calculated separately.

If this is done as one integral, the negative area will cancel out the positive area, and the answer will be wrong.

\(Area = \bigg|\displaystyle\int_b^c{f(x)} dx\bigg| + \displaystyle\int_a^b{f(x)} dx \)



Links to other topics

You may have to calculate points of intersection between the curves to determine the limits for the definite integral.

Curves may be defined parametrically.