The inverse of a function is one that performs the opposite operation to the original function. Inverse functions only exist for one-to-one functions.

The inverse of the function \(f(x)\) is \(f^{-1}(x)\).

When a function is put into its inverse function, or when an inverse function is put into its function, the result is always \(x\):

\(ff^{-1}(x) = f^{-1}f(x) = x\)

Domain and range

The domain of a function is the range of its inverse function.
The range of a function is the domain of its inverse function.

Graphical relationship

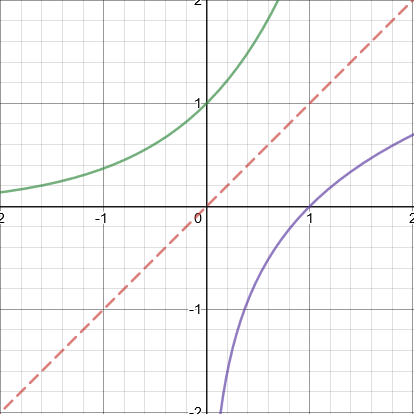
On a graph, an inverse function is the reflection of its function about the \(y=x\) line.

For example, \(f(x)\) is represented by the purple line, \(f^{-1}(x)\) the green line and \(y=x\) the red dashed line.