2.19 Transformations of graphs

AQA Edexcel OCR A OCR B (MEI)
There are three types of transformations:
  • Translations
  • Stretches
  • Reflections

In the examples below, the solid line is the original graph, and the dashed line is the transformed graph.

Translations

\(f(x)+a\): Translation by vector \(\begin{pmatrix} 0 \\ a\end{pmatrix}\) (Translate \(↑\))


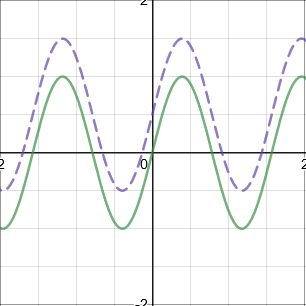
\(f(x)-a\): Translation by vector \(\begin{pmatrix} 0 \\ -a\end{pmatrix}\) (Translate \(↓\))


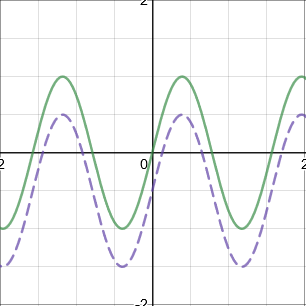
\(f(x+a)\): Translation by vector \(\begin{pmatrix} -a \\ 0\end{pmatrix}\) (Translate \(←\))


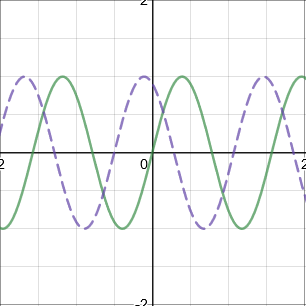
\(f(x-a)\): Translation by vector \(\begin{pmatrix} a \\ 0\end{pmatrix}\) (Translate \(→\))


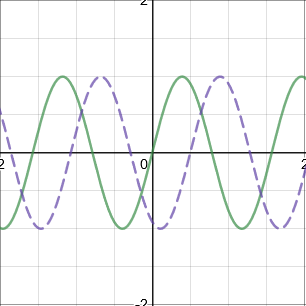
Stretches

\(af(x)\): Stretch parallel to the \(y\)-axis by scale factor \(a\) (Stretch \(\begin{matrix} ↑ \\ ↓\end{matrix}\))


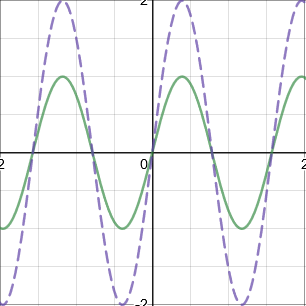
\(\dfrac{1}{a}f(x)\): Stretch parallel to the \(y\)-axis by scale factor \(\dfrac{1}{a}\) (Stretch \(\begin{matrix} ↓ \\ ↑\end{matrix}\))


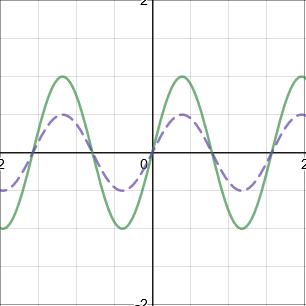
\(f(ax)\): Stretch parallel to the \(x\)-axis by scale factor \(\dfrac{1}{a}\) (Stretch \(→←\))


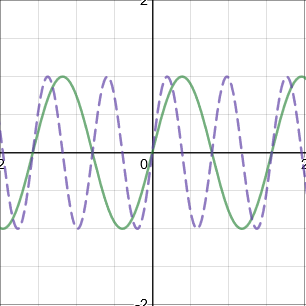
\(f(\dfrac{1}{a}x)\): Stretch parallel to the \(x\)-axis by scale factor \(a\) (Stretch \(←→\))


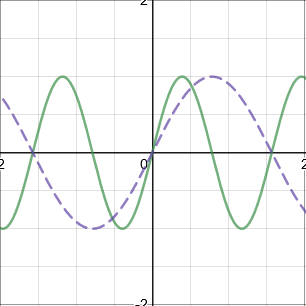
Reflections

\(-f(x)\): Reflection in the \(x\)-axis


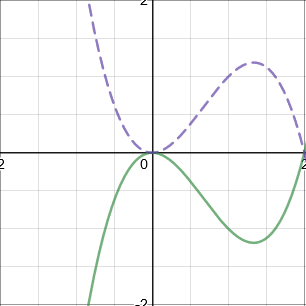
\(f(-x)\): Reflection in the \(y\)-axis



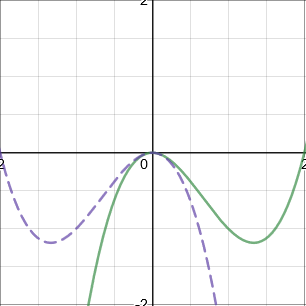
Multiple transformations

Tip: Transformations which involve a combination of translations, stretches and/or reflections, such as \(af(bx+c)+d\) should be done in the following order:

  1. Translate along the \(x\)-axis (move \(c\) units to the left)
  2. Stretch parallel to the \(x\)-axis and reflect in \(y\)-axis if necessary (stretch by scale factor \(\dfrac{1}{b}\) parallel to the \(x\)-axis)
  3. Stretch parallel to the \(y\)-axis and reflect in \(x\)-axis if necessary (stretch by scale factor \(a\) parallel to the \(y\)-axis)
  4. Translate along the \(y\)-axis (move \(d\) units up)

You should be able to apply these transformations to any of the functions covered in the syllabus:

  • quadratics, cubics, quartics
  • reciprocals
  • modulus
  • \(\sin{x}\), \(\cos{x}\), \(\tan{x}\)
  • \(e^x\), \(a^x\)
Important
Summary of transformations:

Translations:

\(f(x)+a\): Translate \(↑\)
\(f(x)-a\): Translate \(↓\)
\(f(x+a)\): Translate \(←\)
\(f(x-a)\): Translate \(→\)

Stretches:

\(af(x)\): Stretch \(\begin{matrix} ↑ \\ ↓\end{matrix}\)
\(\dfrac{1}{a}f(x)\): Stretch \(\begin{matrix} ↓ \\ ↑\end{matrix}\)
\(f(ax)\): Stretch \(→←\)
\(f(\dfrac{1}{a}x)\): Stretch \(←→\)

Reflections:

\(-f(x)\): Reflection in the \(x\)-axis
\(f(-x)\): Reflection in the \(y\)-axis

Multiple transformations:

Translate in \(x\) direction, stretch/reflect in \(x\) direction, stretch/reflect in \(y\) direction, translate in \(y\) diretcion
3