Logarithms are the inverse of exponentials.

If \(f(x) = a^x \), then \(f^{-1}(x) = \log_a{x} \).

Alternatively:

\(a^x = y \iff x = \log_a{y} \)

where \(a > 0\), \(a \neq 1\) and \(x ≥ 0\).

\(\log_a{y}\) is pronounced "\(\log\) base \(a\) of \(y\)".

Where the base is omitted, i.e. \(\log{y}\), the base is assumed to be \(10\).

Natural logarithms

When the base is the natural base \(e\), i.e. \(\log_e\), there is a special notation: \(\ln\).

Accordingly, if \(f(x) = e^x \), then \(f^{-1}(x) = \ln{x} \).

Alternatively:

\(e^x = y \iff x = \ln{y} \)

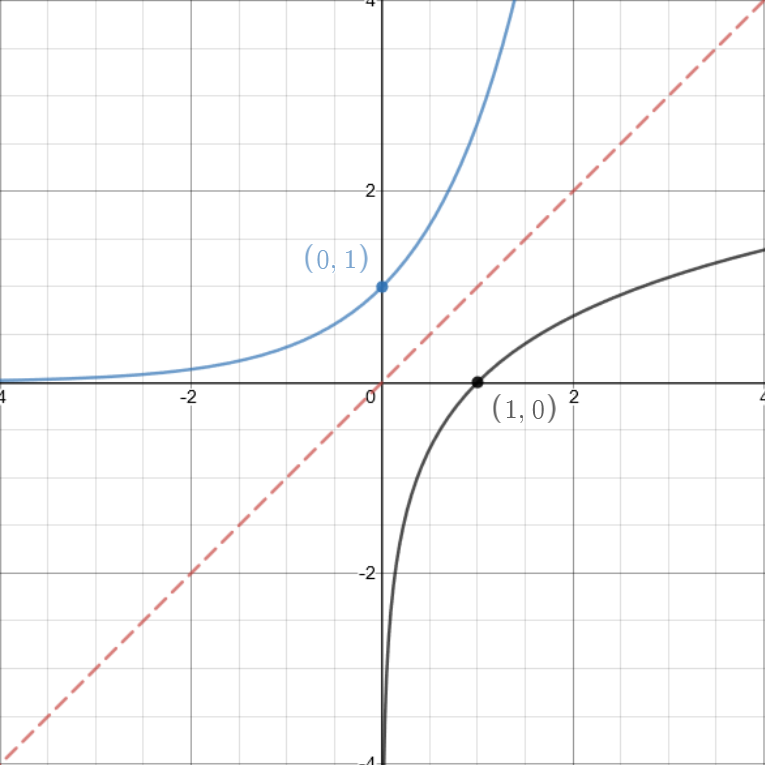
Graph of the natural logarithm

\(y=\ln{x} \quad \textcolor{blue}{y=e^x} \)