Addition formulae

The addition formulae can be derived from the diagram below:



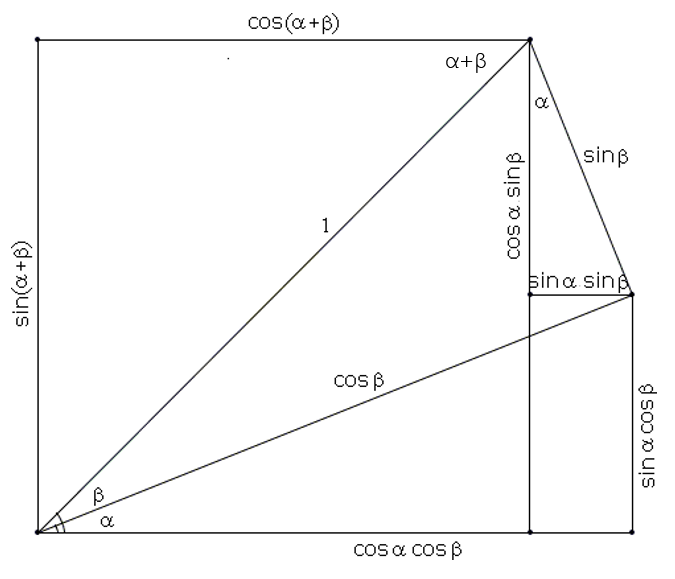
\(\implies \boxed{\sin{(A+B)} ≡ \sin{A}\cos{B} + \cos{A}\sin{B}}\)

\(\implies \boxed{\cos{(A+B)} ≡ \cos{A}\cos{B} - \sin{A}\sin{B}}\)

Applying the identity: \(\tan{\theta} ≡ \dfrac{\sin{\theta}}{\cos{\theta}}\)

\(\implies \tan{(A+B)} ≡ \dfrac{\sin{A}\cos{B} + \cos{A}\sin{B}}{\cos{A}\cos{B} - \sin{A}\sin{B}}\)

Dividing all terms by \(\cos{A}\cos{B}\):

\(\implies \tan{(A+B)} ≡ \dfrac{\dfrac{\sin{A}\cancel{\cos{B}}}{\cos{A}\cancel{\cos{B}}} + \dfrac{\cancel{\cos{A}}\sin{B}}{\cancel{\cos{A}}\cos{B}}} {\dfrac{\cancel{\cos{A}\cos{B}}}{\cancel{\cos{A}\cos{B}}} - \dfrac{\sin{A}\sin{B}}{\cos{A}\cos{B}}}\)

\(\implies \boxed{\tan{(A+B)} ≡ \dfrac{\tan{A} + \tan{B}}{1 - \tan{A}\tan{B}}}\)

Substituting \(-B\) into \(B\) gives the negative versions:

\(\implies \boxed{\sin{(A-B)} ≡ \sin{A}\cos{B} - \cos{A}\sin{B}}\)

\(\implies \boxed{\cos{(A-B)} ≡ \cos{A}\cos{B} + \sin{A}\sin{B}}\)

\(\implies \boxed{\tan{(A-B)} ≡ \dfrac{\tan{A} - \tan{B}}{1 + \tan{A}\tan{B}}}\)

These are provided in the formula book.

Double angle formulae

Substituting \(A\) into \(B\) for the addition formulae gives the double angle formulae:

\(\sin{(A+A)} ≡ \sin{A}\cos{A} + \cos{A}\sin{A}\)

\(\implies \boxed{\sin{2A} ≡ 2\sin{A}\cos{A}}\)

\(\cos{(A+A)} ≡ \cos{A}\cos{A} - \sin{A}\sin{A}\)

\(\implies \boxed{\cos{2A} ≡ \cos^2{A} - \sin^2{A}}\)

\(\tan{(A+B)} ≡ \dfrac{\tan{A} + \tan{B}}{1 - \tan{A}\tan{B}}\)

\(\implies \boxed{\tan{2A} ≡ \dfrac{2\tan{A}}{1 - \tan^2{A}}}\)

Applying the identity \(\sin^2{\theta}+\cos^2{\theta}=1\) to \(\cos{2A}\) provides two further forms:

\(\cos{2A} ≡ (1 - \sin^2{A}) - \sin^2{A}\)

\(\implies \boxed{\cos{2A} ≡ 1 - 2\sin^2{A}}\)

\(\cos{2A} ≡ \cos^2{A} - (1 - \cos^2{A})\)

\(\implies \boxed{\cos{2A} ≡ 2\cos^2{A} - 1}\)

These are provided in the formula book.