\(\boxed{\tan{\theta}≡\dfrac{\sin{\theta}}{\cos{\theta}}}\)

Applying the reciprocal function: \(\cot{\theta}≡\dfrac{1}{\tan{\theta}}\)

\(\implies \boxed{\cot{\theta}≡\dfrac{\cos{\theta}}{\sin{\theta}}}\)

Consider the right angle triangle with hypotenuse of length \(1\):



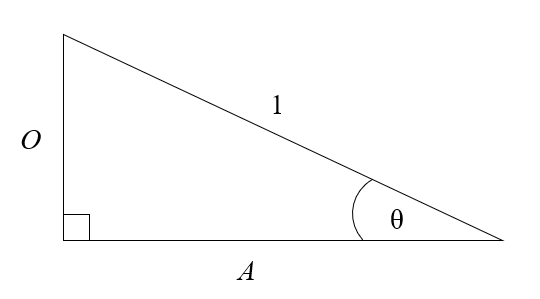
\(\sin{\theta}≡\dfrac{O}{1} \quad \cos{\theta}≡\dfrac{A}{1}\)

Applying Pythagoras' Theorem: \(O^2+A^2=1^2\)

\(\implies \boxed{\sin^2{\theta}+\cos^2{\theta} = 1}\)

Dividing by \(\cos^2{\theta}\): \(\dfrac{\sin^2{\theta}}{\cos^2{\theta}}+\dfrac{\cos^2{\theta}}{\cos^2{\theta}} = \dfrac{1}{\cos^2{\theta}}\)

\(\implies \boxed{\tan^2{\theta}+1 = \sec^2{\theta}}\)

Dividing by \(\sin^2{\theta}\): \(\dfrac{\sin^2{\theta}}{\sin^2{\theta}}+\dfrac{\cos^2{\theta}}{\sin^2{\theta}} = \dfrac{1}{\sin^2{\theta}}\)

\(\implies \boxed{1+\cot^2{\theta} = \cosec^2{\theta}}\)

These identities can be used to solve trigonometric equations and to prove further identities.