Vector addition

Triangle law for vector addition:



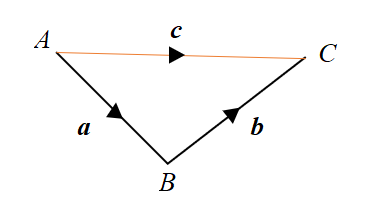
\(\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC} \)

If \(\overrightarrow{AB} = \bold{a}\), \(\overrightarrow{BC} = \bold{b}\) and \(\overrightarrow{AC} = \bold{c}\), then:

\(\bold{a} + \bold{b} = \bold{c} \)

Parallelogram law for vector addition:



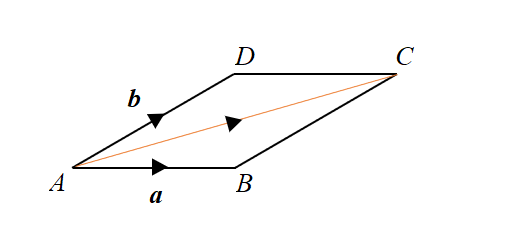
\(\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC} \)

\(\overrightarrow{BC} = \overrightarrow{AD} \)

\(\implies \bold{a} + \bold{b} = \overrightarrow{AC} \)

In column vector form:

\(\begin{pmatrix} p \\ q \end{pmatrix} + \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} p+r \\ q+s \end{pmatrix} \)

Vector subtraction

Subtracting a vector is the equivalent of adding the reverse of a vector

\(\bold{a} - \bold{b} = \bold{a} + (-\bold{b}) \)

Multiplication by a scalar

\(\lambda \begin{pmatrix} p \\ q \end{pmatrix} = \begin{pmatrix} \lambda p \\ \lambda q \end{pmatrix} \)