#9.2.1
Classification by luminosity
Apparent magnitude, m.
The Hipparcos scale.
Dimmest visible stars have a magnitude of 6.
Relation between brightness and apparent magnitude. Difference of 1 on magnitude scale is equal to an intensity ratio of 2.51.
Brightness is a subjective scale of measurement.
#9.2.2
Absolute magnitude, M
Parsec and light year.
Definition of M, relation to m:
\(m - M = 5\log{\dfrac{d}{10}} \)
#9.2.3
Classification by temperature, black-body radiation
Stefan’s law and Wien’s displacement law.
General shape of black-body curves, use of Wien’s displacement law to estimate black-body temperature of sources.
Experimental verification is not required.
\(λ_{max}T = constant = 2.9 × 10^{-3} m K \)
Assumption that a star is a black body.
Inverse square law, assumptions in its application.
Use of Stefan’s law to compare the power output, temperature and size of stars
\(P = σAT^4 \)
#9.2.4
Principles of the use of stellar spectral classes
Description of the main classes:
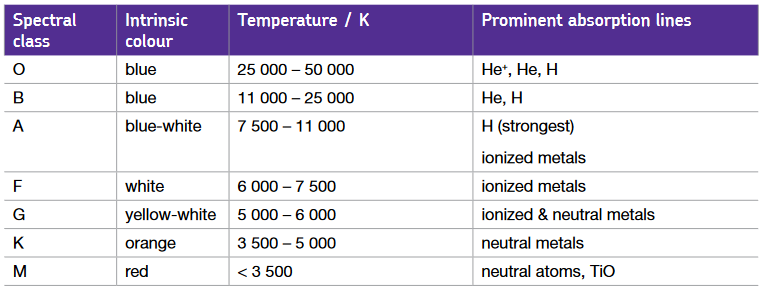
Temperature related to absorption spectra limited to Hydrogen Balmer absorption lines: requirement for atoms in an \(n = 2\) state.
#9.2.5
The Hertzsprung-Russell (HR) diagram
General shape: main sequence, dwarfs and giants.
Axis scales range from –10 to +15 (absolute magnitude) and 50 000 K to 2 500 K (temperature) or OBAFGKM (spectral class).
Students should be familiar with the position of the Sun on the HR diagram.
Stellar evolution: path of a star similar to our Sun on the HR diagram from formation to white dwarf.
#9.2.6
Supernovae, neutron stars and black holes
Defining properties: rapid increase in absolute magnitude of supernovae; composition and density of neutron stars; escape velocity > c for black holes.
Gamma ray bursts due to the collapse of supergiant stars to form neutron stars or black holes.
Comparison of energy output with total energy output of the Sun.
Use of type 1a supernovae as standard candles to determine distances. Controversy concerning accelerating Universe and dark energy.
Students should be familiar with the light curve of typical type 1a supernovae.
Supermassive black holes at the centre of galaxies.
Calculation of the radius of the event horizon for a black hole, Schwarzschild radius (Rs),
\(R_s ≈ \dfrac{2GM}{c^2} \)