The trapezium rule can be used to find the approximate area under a curve for functions which are impossible to integrate algebraically.

Consider the graph below of \(y=f(x)\).



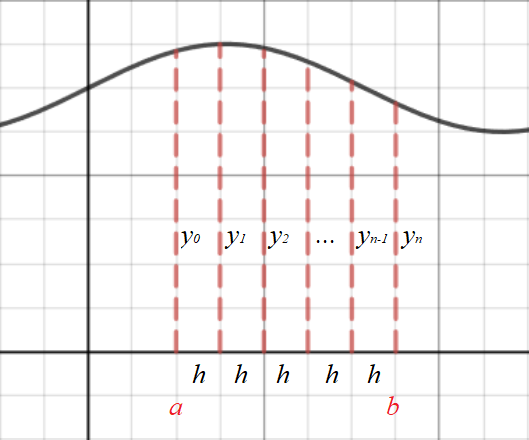
The area under the curve from \(x=a\) to \(x=b\) can be split into \(n\) strips (trapeziums).

The sum of the areas of the trapeziums is an approximation of the area under the curve, i.e. \(\displaystyle\int_a^b{y} dx \).

The width of each strip (\(h\)) is calculated by \(h = \dfrac{b-a}{n}\).

The height of the boundary of each strip can be calculated by working out \(y_0 = f(a)\), \(y_1 = f(a+h)\), \(y_2 = f(a+2h)\), etc

The area of one strip can be calculated by using the formula for the area of a trapezium, e.g. for the first strip:

\(Area = \dfrac{1}{2}h(y_0+y_1) \)

The area of all the strips (an approximation of the area under the curve) is therefore:

\(\displaystyle\int_a^b{y} dx \approx \dfrac{1}{2}h(y_0+y_1) + \dfrac{1}{2}h(y_1+y_2) + ... + \dfrac{1}{2}h(y_{n-1}+y_n)\)

Factorising out \(\dfrac{1}{2}h\) gives:

\(\displaystyle\int_a^b{y} dx \approx \dfrac{1}{2}h(y_0 + y_1 + y_1 + y_2 + y_2 + ... + y_{n-1} + y_{n-1} + y_n)\)

\(\implies \boxed{\displaystyle\int_a^b{y} dx \approx \dfrac{1}{2}h(y_0 + 2(y_1 + y_2 + ... + y_{n-1}) + y_n)} \)

Tip: This formula is provided in the formula book but you need to know how to use it.