The sine and cosine rules can be used for any triangle.



Sine rule

\(\dfrac{a}{\sin{A}}=\dfrac{b}{\sin{B}}=\dfrac{c}{\sin{C}}\)

Tip: Use the sine rule when there are 2 opposing angles and sides involved.

For example, this could be 2 known sides, 1 known angle, and 1 unknown angle; or 2 known angles, 1 known side and 1 unknown side.

Cosine rule

\(a^2=b^2+c^2-2bc\cos{A}\)

Tip: Use the cosine rule when there are 3 sides and 1 angle involved.

For example, this could be 3 known sides and 1 unknown angle; or 2 known sides, 1 known angle formed from those sides, and 1 unknown side opposite the angle.

Some questions may require the use of both the sine and cosine rules.

Area of a triangle

\(Area = \dfrac{1}{2}ab\sin{C}\)

The ambiguous case



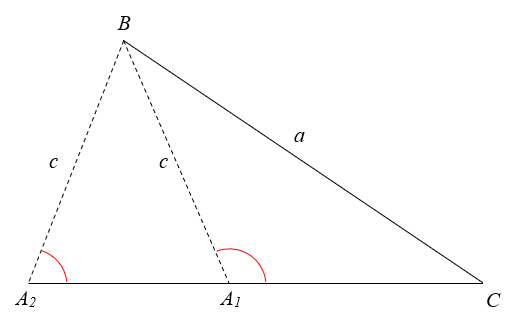
When given sides \(a\) and \(c\) and angle \(C\), it is possible to draw the triangle in two different ways.

You can draw \(c\) such that the angle at \(A\) is obtuse (\(A_1\)), or acute (\(A_2\)).

Therefore it is possible for the sine rule to sometimes produce two solutions for a missing angle, since:

\(\sin{θ} = \sin{(180\degree-θ)}\)