Product moment correlation coefficient

The product moment correlation coefficient (PMCC) (\(r\)) describes the linear correlation between two variables, and can take any value between \(-1\) and \(1\) inclusive.

When \(r=1\), there is a perfect positive linear corrleation. All the data points lie on a straight line with a positive gradient.
When \(r=-1\), there is a perfect negative linear corrleation.All the data points lie on a straight line with a negative gradient.
When \(r=0\), there is no linear correlation.

Hypothesis testing for zero correlation

\(r\) is the PMCC for a sample, and \(\rho\) is the PMCC for a population.

You can use a hypothesis test to test whether the PMCC for a sample (\(r\)) indicates that there is likely to be a linear relationship in the population.

For a one-tailed test:

\(H_0:\rho=0\)
\(H_1:\rho > 0\) or \(H_1:\rho < 0\)

For a two-tailed test:

\(H_0:\rho=0\)
\(H_1:\rho \neq 0\)

To carry out the test, you will need to compare your \(r\) value with the table of critical values for a given significance level (usually \(5%\)) and sample size. The table of critical values are provided in the formula book.



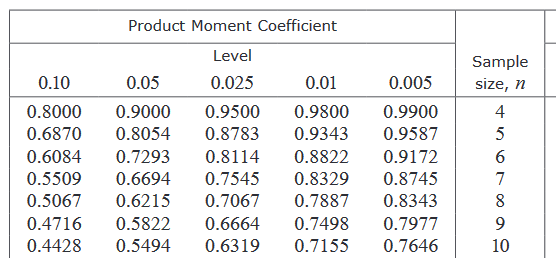
An observed value of \(r\) greater than the critical value would provide sufficient evidence to reject the null hypothesis and conclude that it is likely that \(\rho>0\).

An observed value of \(r\) less than the negative of the critical value would provide sufficient evidence to reject the null hypothesis and conclude that it is likely that \(\rho<0\).