First law of thermodynamics

Quantitative treatment of first law of thermodynamics, \(Q = ∆U + W \)

where Q is energy transferred to the system by heating, ∆U is increase in internal energy and W is work done by the system.

Applications of first law of thermodynamics.

Non-flow processes

Isothermal, adiabatic, constant pressure and constant volume changes.

\(pV = nRT \)

adiabatic change: \(pV^γ = constant \)

isothermal change: \(pV = constant \)

at constant pressure \(W = pΔV \)

Application of first law of thermodynamics to the above processes.

The p–V diagram

Representation of processes on p–V diagram.

Estimation of work done in terms of area below the graph.

Extension to cyclic processes: work done per cycle = area of loop

Expressions for work done are not required except for the constant pressure case, \(W = pΔV \)

Engine cycles

Understanding of a four-stroke petrol engine cycle and a diesel engine cycle, and of the corresponding indicator diagrams.

Comparison with the theoretical diagrams for these cycles; use of indicator diagrams for predicting and measuring power and efficiency

input  power = calorific value × fuel flow rate

Indicated power as (area of p−V loop) × (no. of cycles per second) × (no. of cylinders)

Output or brake power, \(P = Tω \)

friction power = indicated power – brake power

Engine efficiency; overall, thermal and mechanical efficiencies.

\(\text{Overall efficiency} = \dfrac{\text{brake power}}{\text{input power}} \)

\(\text{Thermal efficiency} = \dfrac{\text{indicated power}}{\text{input power}} \)

\(\text{Mechanical efficiency} = \dfrac{\text{brake power}}{\text{indicated power}} \)

A knowledge of engine constructional details is not required.

Questions may be set on other cycles, but they will be interpretative and all essential information will be given.

Second Law and engines

Impossibility of an engine working only by the First Law.

Second Law of Thermodynamics expressed as the need for a heat engine to operate between a source and a sink.

efficiency \(= \dfrac{W}{Q_H} = \dfrac{Q_H - Q_C}{Q_H} \)

maximum theoretical efficiency \(= \dfrac{T_H - T_C}{T_H} \)



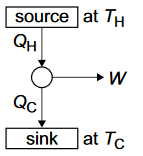
Reasons for the lower efficiencies of practical engines.

Maximising use of W and Q_H for example in combined heat and power schemes.

Reversed heat engines

Basic principles and uses of heat pumps and refrigerators.

A knowledge of practical heat pumps or refrigerator cycles and devices is not required.



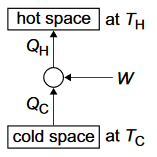
Coefficients of performance:

refrigerator: \(COP_{ref} = \dfrac{Q_C}{W} = \dfrac{Q_C}{Q_H-Q_C} = \dfrac{T_C}{T_H-T_C} \)

heat pump: \(COP_{hp} = \dfrac{Q_H}{W} = \dfrac{Q_H}{Q_H-Q_C} = \dfrac{T_H}{T_H-T_C} \)